
题目列表(包括答案和解析)
 点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求:
点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求: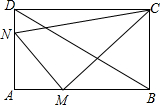 点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求:
点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求:如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内
分别标有数字1、2、-3、-4.指针固定,转动转盘后任其自由停止,指针所指扇形得到相
应位置上的数字(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇
形内).
1.若将转盘转动一次,求得到负数的概率;
2.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b.请你用列表法或树状图求a与 b都是方程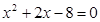 的解的概率.
的解的概率.

【解析】
3.让负数的个数除以数的总个数即可;
4.求出方程的解,根据列表法或树状图求进行解答
如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内
分别标有数字1、2、-3、-4.指针固定,转动转盘后任其自由停止,指针所指扇形得到相
应位置上的数字(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇
形内).
1.若将转盘转动一次,求得到负数的概率;
2.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b.请你用列表法或树状图求a与 b都是方程![]() 的解的概率.
的解的概率.

【解析】
3.让负数的个数除以数的总个数即可;
4.求出方程的解,根据列表法或树状图求进行解答
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com