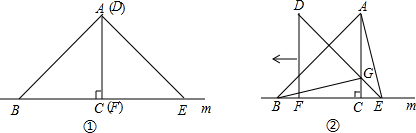如图：已知反比例C₁：y=

k1

x

；C₂：y=

k2

x

，且k₁＞k₂＞0，点P是双曲线C₁上的一点，过P点引x、y轴的平行线交双曲线C₂于A、B两点，连接AB．
（1）当取k₁=4，k₂=1，
①点P坐标为（2，2）时，则S_三角形ABP=；
②点P坐标为（1，4）时，S_三角形ABP=．
（2）通过观察、思考（1）的计算结果，你能猜想到△ABP的面积有何规律或特征？并请你用含k₁、k₂的代数式表示△ABP的面积．

如图，四边形ABCD是正方形，点E是CD上一点，点F是CB延长线上一点，且DE=BF，通过观察与思考可以知道△AFB可以看作是绕，顺时针旋转得到△AEF是三角形．

9、妙趣角：辅助线
问题探讨实录片段：
老师：等腰三角形的两个底角一定相等吗？
同学们异口同声：一定相等！
老师：谁能说说理由？[说着，在图（1）上用符号分别表示了已知“等腰”的条件和“底角为何相等”的疑问．]
小明：如图（2），如果作顶角平分线AD，那么可以根据“SAS”知道△ABD≌△ACD，得到∠B=∠C．
小华：如图（3），如果作底边上的中线，那么可以根据“SSS”，知道△ABD≌△ACD，得到∠B=∠C．
小芳：如图（4），如果作底边上的高，那么可以根据“HL”，知道△ABD≌△ACD，得到∠B=∠C．
老师：非常好！小明、小华和小芳所作的线段虽然名目各异，但是作用相同──都是通过构造一对全等三角形来说明∠B=∠C，所画的这条线段AD，可以称它为“辅助线”．
小强：“辅助线”，可谓名副其实．
老师：上面大家探讨得到：一个三角形中，如果知道两边相等，那么可得这两边的对角也相等，这可简述为“等边对等角”．
小霞：我想也应该有“等角对等边”[说着，画出了图（5），其中，AB、AC两边上的“”无疑也是在征求说理．]
不一会，争先恐后的几位同学在黑板上画出了如下带有“辅助线”的图形[图（6）、（7）、（8）]：

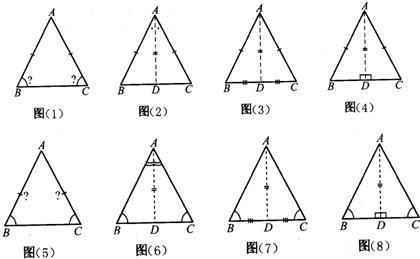
老师期待的目光显然是在说：请你通过观察与思考，对上述3个图形作一评价…

19、《天天伴我学数学》一道作业题．如图1：请你想办法求出五角星中∠A+∠B+∠C+∠D+∠E的值．由于刚涉及到几何证明，很多学生不知道如何求出其结果．下面是习题讲解时，老师和学生对话的情景：老师向学生抛出问题：①观察图象，各个角的度数能分别求出他们的度数吗，能的话怎么求，不能的话怎么办？学生通过观察回答：很明显每个角都不规则，求不出各个角的度数．有个学生小声的说了句：要是能把这五个角放到一块就好了？老师回答：有想法，就去试试看．很快就有学生发现利用三角形外角性质将∠C和∠E；∠B和∠D分别用外角∠1和∠2表示．于是得到∠A+∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°．根据以上信息，亲爱的同学们，你能求出图2中∠A+∠B+∠C+∠D+∠E+∠F+∠G的值吗？请给予证明．