
题目列表(包括答案和解析)
| e |
| 1 |
| 4 |
| e |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数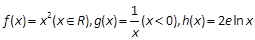 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
 递减;
递减; ;
; .
. 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题: 在
在 内单调递增;
内单调递增; 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4; 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
; 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.| A.1个 | B.2个 | C.3个 | D.4个 |
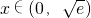 递减;
递减; ;
;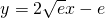 .
.
一、选择题:(本大题共12小题每小题5分,共60分)
AADCB DDBCC DC
二、填空题:(共4小题,每小题4分,共16分)
13. 14.20 15.32 16.
14.20 15.32 16.
三、解答题:(共6小题,共74分)
17.解:(1) ………………2分
………………2分
 .………………………………4分
.………………………………4分
在[0,π]上单调递增区间为 .…………………6分
.…………………6分
(2) ,
,
当x=0时, ,………………………………………8分
,………………………………………8分
由题设知 …………………………………………10分
…………………………………………10分
解之,得 …………………………………………12分
…………………………………………12分
|