
题目列表(包括答案和解析)
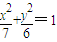 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为 .
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为 .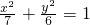 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为________.
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为________.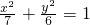 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,…),使|PF1|,|PF2|,|PF3|…组成公差为d的等差数列,则d的取值范围是
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,…),使|PF1|,|PF2|,|PF3|…组成公差为d的等差数列,则d的取值范围是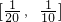
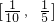
 ∪
∪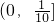
 ∪
∪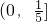
 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为( )。
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为( )。
一.选择题
(1)D (2)A (3)B (4)C (5)B (6)C
(7)B (8)C (9)A (10)C (11)B (12)D
二.填空题
(13)4 (14)0.75 (15)9 (16).files\image125.png)
三.解答题
(17)解:由.files\image127.png)
.files\image129.png)
得 .files\image131.png) 又
又.files\image133.png)
于是 .files\image135.png)
.files\image137.png)
(18)解:(Ⅰ)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.
|