
题目列表(包括答案和解析)
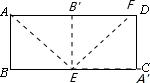 18、当身边没有量角器时,可以通过动手操作得到一些特定的角度.如图,已知矩形ABCD,按如下步骤操作可以得到一个特定的角度.(1)以过点A所在的直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于点E.(2)将纸片返回展平后,再一次折叠纸片,以过点E所在的直线为折痕,使点A落在BC上,折痕EF交AD于点F,则∠DFE=
18、当身边没有量角器时,可以通过动手操作得到一些特定的角度.如图,已知矩形ABCD,按如下步骤操作可以得到一个特定的角度.(1)以过点A所在的直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于点E.(2)将纸片返回展平后,再一次折叠纸片,以过点E所在的直线为折痕,使点A落在BC上,折痕EF交AD于点F,则∠DFE= .小明按键输入
.小明按键输入 显示结果为4,则他按键
显示结果为4,则他按键 输入显示结果应为
输入显示结果应为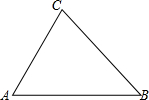 如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边. (2012•六合区一模)观察猜想
(2012•六合区一模)观察猜想湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com