
题目列表(包括答案和解析)
(本小题满分15分)
已知函数![]() ,其中
,其中![]() ,
,![]() (
(![]() ),若
),若![]() 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于![]() .
.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)在![]() 中,
中,![]() 分别是角
分别是角![]() 的对边,
的对边,![]() ,当
,当![]() 最大时,
最大时,![]() ,求
,求![]() 的面积.
的面积.
(本小题满分15分)
 某旅游商品生产企业,2009年某商品生产的投入成本为1元/件,
某旅游商品生产企业,2009年某商品生产的投入成本为1元/件,
出厂价为流程图的输出结果![]() 元/件,年销售量为10000件,
元/件,年销售量为10000件,
因2010年国家长假的调整,此企业为适应市场需求,
计划提高产品档次,适度增加投入成本.若每件投入成本增加的
比例为![]() (
(![]() ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为![]() ,
,
同时预计销售量增加的比例为![]() .
.
已知得利润![]() (出厂价
(出厂价![]() 投入成本)
投入成本)![]() 年销售量.
年销售量.
(Ⅰ)写出2010年预计的年利润![]()
与投入成本增加的比例![]() 的关系式;
的关系式;
(Ⅱ)为使2010年的年利润比2009年有所增加,
问:投入成本增加的比例![]() 应在什么范围内?
应在什么范围内?
(本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(1)设![]() ,把y表示成
,把y表示成![]() 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?

(本小题满分15分)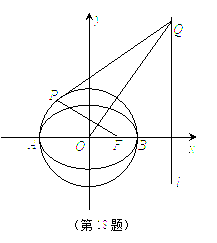 如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为![]() 的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
(2)证明:直线PQ与圆O相切.
(本小题满分15分)已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足![]() ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
1
2
3
4
5
6
7
8
2


9
充分不必要

4
①②④
9
10
11
12
13
14


 或0
或0
点P在圆内

①②③
15.解: (1)因为各组的频率和等于1,故低于50分的频率为:

所以低于50分的人数为 (人)………………………………………….5分
(人)………………………………………….5分
(2)依题意,成绩60及以上的分数所在的第三、四、五、六组(低于50分的为第一组),
频率和为 
所以,抽样学生成绩的合格率是 %.
%.
于是,可以估计这次考试物理学科及格率约为 %……………………………………9分.
%……………………………………9分.
(3)“成绩低于50分”及“[50,60)”的人数分别是6,9。所以从成绩不及格的学生中选两人,他们成绩至少有一个不低于50分的概率为: ……………14分
……………14分
16.解:(1) ,
,
即 ,
,
∴ ,∴
,∴ .
.
∵ ,∴
,∴ .………………………………………………………………7分
.………………………………………………………………7分
(2)m n
n  ,
,
 |m
|m n|
n| .
.
∵ ,∴
,∴ ,∴
,∴ .
.
从而 .
.
∴当 =1,即
=1,即 时,|m
时,|m n|
n| 取得最小值
取得最小值 .
.
所以,|m n|
n| .………………………………………………………………14分
.………………………………………………………………14分
17.(1)证明: E、P分别为AC、A′C的中点,
E、P分别为AC、A′C的中点,
 EP∥A′A,又A′A
EP∥A′A,又A′A 平面AA′B,EP
平面AA′B,EP 平面AA′B
平面AA′B
∴即EP∥平面A′FB …………………………………………7分
(2) 证明:∵BC⊥AC,EF⊥A′E,EF∥BC
∴BC⊥A′E,∴BC⊥平面A′EC
BC 平面A′BC
平面A′BC
∴平面A′BC⊥平面A′EC …………………………………………14分
注:直角三角形条件在证这两问时多余了,可直接用两侧面的直角三角形证明即可。
18.解:(1)取弦的中点为M,连结OM
由平面几何知识,OM=1
 得:
得: ,
,
∵直线过F、B ,∴ 则
则 …………………………………………6分
…………………………………………6分
(2)设弦的中点为M,连结OM
则
 解得
解得

∴ …………………………………………15分
…………………………………………15分
(本题也可以利用特征三角形中的有关数据直接求得)
 19.
19.
 |
第(3)问的构造法可直接用第二种方法,作差后用 代换
代换 即可。
即可。
20.解:(1)由方程组 的解为
的解为 不符合题设,可证。………3分
不符合题设,可证。………3分
(2)假设存在。
由方程组 ,得
,得 ,即
,即 …5分
…5分
设 (
( ),可证:当
),可证:当 时,
时, 单调递减且
单调递减且 ;当
;当 时,
时, 单调递减且
单调递减且 。
。
 ,设
,设 ,则
,则 。………7分
。………7分
①当 时,
时, ,
, 递增,故
递增,故 ,
,
于是 ,
, 在
在 上单调递减。
上单调递减。
设 ,则
,则 ,
, 在
在 上递增,
上递增, ,即
,即 ,所以
,所以 。………9分
。………9分
②当 时,
时, ,
, 递减,故
递减,故 ,
,
于是 ,
, 在
在 上单调递减。
上单调递减。
 ,
, 在
在 上递减,
上递减, ,即
,即 ,所以
,所以
由函数 (
( )的性质可知满足题设的
)的性质可知满足题设的 不存在。………11分
不存在。………11分
(3)假设1, ,
, 是一个公差为
是一个公差为 的等差数列的第r、s、t项,又是一个等比为
的等差数列的第r、s、t项,又是一个等比为 等比数列的第r、s、t项。于是有:
等比数列的第r、s、t项。于是有: ,
,
 ,
,
从而有 , 所以
, 所以 。
。
设 ,同(2)可知满足题设的
,同(2)可知满足题设的 不存在………16分
不存在………16分
注:证法太繁,在第二问中,可用 来表示,消去
来表示,消去 可得
可得 ,则构造
,则构造 易得到极值点为
易得到极值点为 。
。
附加题参考答案
附1.(1)设M= ,则有
,则有
 =
= ,
,
 =
= ,
,
所以 且
且 解得
解得 ,所以M=
,所以M= .…………………………5分
.…………………………5分
(2)任取直线l上一点P(x,y)经矩阵M变换后为点P’(x’,y’).
因为 ,所以又m:
,所以又m: ,
,
所以直线l的方程(x+2y)-(3x+4y)=4,即x+y+2=0.………………………………10分
附2.解:以有点为原点,极轴为 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1) ,
, ,由
,由 得
得 .
.
所以 .
.
即 为圆
为圆 的直角坐标方程.
的直角坐标方程.
同理 为圆
为圆 的直角坐标方程.
……………………………………6分
的直角坐标方程.
……………………………………6分
(2)由
相减得过交点的直线的直角坐标方程为 .
…………………………10分
.
…………………………10分
附3.(1)设P(x,y),根据题意,得 .
.
化简,得 .………………………………………………………………5分
.………………………………………………………………5分
(2) .……………………………………10分
.……………………………………10分
附4.(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知 ………………………………4分
………………………………4分
(2)ξ可取1,2,3,4.  ,
,
 ;………………8分
;………………8分
故ξ的分布列为
ξ
1
2
3
4
P




 答:ξ的数学期望为
答:ξ的数学期望为 …………10分
…………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com