问题提出:以n边形的n个顶点和它内部的m个点,共(m+n)个点为顶点,可把原n边形分割成多少个互不重叠的小三角形?
问题探究:为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手,通过观察、分析,最后归纳出结论:
探究一:以△ABC的三个顶点和它内部的一个点P,共4个点为顶点,可把△ABC分割成多少个互不重叠的小三角形?
如图(1),显然,此时可把△ABC分割成3个互不重叠的小三角形.
探究二:以△ABC的三个顶点和它内部的2个点P、Q,共5个点为顶点,可把△ABC分割成多少个互不重叠的小三角形?
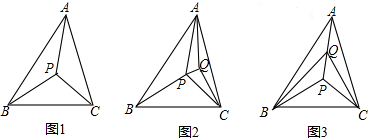
在探究一的基础上,我们可看作在图(1)△ABC的内部,再添加1个点Q,那么点Q的位置会有两种情况:一种情况,点Q在图(1)分割成的某个小三角形内部,不妨假设点Q在△PAC内部,如图(2);另一种情况,点Q在图(1)分割成的小三角形的某条公共边上,不妨假设点Q在P上,如图(3);显然,不管哪种情况,都可把△ABC分割成5个互不重叠的小三角形.
探究三:以△ABC的三个顶点和它内部的3个点,共6个点为顶点可把△ABC分割成
7
7
个互不重叠的小三角形.
探究四:以△ABC的三个顶点和它内部的m个点,共(m+3)个点为顶点可把△ABC分割成
3+2(m-1)或2m+1
3+2(m-1)或2m+1
个互不重叠的小三角形.
探究拓展:以四边形的4个顶点和它内部的m个点,共(m+4)个点为顶点,可把四边形分割成
4+2(m-1)或2m+2
4+2(m-1)或2m+2
个互不重叠的小三角形.
问题解决:以n边形的n个顶点和它内部的m个点,共(m+n)个点为顶点,可把△ABC分割成
n+2(m-1)或2m+n-
n+2(m-1)或2m+n-
个互不重叠的小三角形.
实际应用:以八边形的8个顶点和它内部的m个点,共(m+8)个点为顶点,可把八边形分割成2013个互不重叠的小三角形吗?若行,求出m的值;若不行,请说明理由.