在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5.
（Ⅰ)探究新知：
如图①⊙O是△ABC的内切圆，与三边分别相切于点E、F、G..
（1）求证内切圆的半径r₁="1;"
（2）求tan∠OAG的值；
（Ⅱ）结论应用
（1）如图②若半径为r₂的两个等圆⊙O₁、⊙O₂外切，且⊙O₁与AC、AB相切，⊙O₂与BC、AB相切，求r₂的值；
（2）如图③若半径为r_n的n个等圆⊙O₁、⊙O₂、…、⊙O_n依次外切，且⊙O₁与AC、AB相切，⊙O_n与BC、AB相切，⊙O₁、⊙O₂、…、⊙O_n均与AB相切，求r_n的值.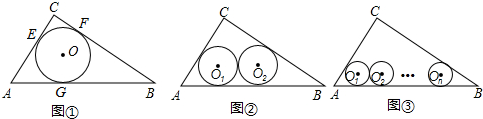

在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5.

（Ⅰ)探究新知：

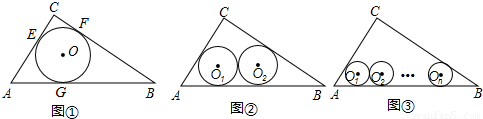
如图① ⊙O是△ABC的内切圆，与三边分别相切于点E、F、G..

（1）求证内切圆的半径r₁=1;

（2）求tan∠OAG的值；

（Ⅱ）结论应用

（1）如图②若半径为r₂的两个等圆⊙O₁、⊙O₂外切，且⊙O₁与AC、AB相切，⊙O₂与BC、AB相切，求r₂的值；

（2）如图③若半径为r_n的n个等圆⊙O₁、⊙O₂、…、⊙O_n依次外切，且⊙O₁与AC、AB相切，⊙O_n与BC、AB相切，⊙O₁、⊙O₂、…、⊙O_n均与AB相切，求r_n的值.

在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5.

（Ⅰ)探究新知

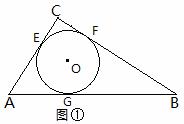
如图① ⊙O是△ABC的内切圆，与三边分别相切于点E、F、G..

（1）求证内切圆的半径r₁=1;

（2）求tan∠OAG的值；

（Ⅱ）结论应用

（1）如图②若半径为r₂的两个等圆⊙O₁、⊙O₂外切，且⊙O₁与AC、AB相切，⊙O₂与BC、AB相切，求r₂的值；

（2）如图③若半径为r_n的n个等圆⊙O₁、⊙O₂、…、⊙O_n依次外切，且⊙O₁与AC、AB相切，⊙O_n与BC、AB相切，⊙O₁、⊙O₂、…、⊙O_n均与AB相切，求r_n的值.

定义：三边长与面积都是整数的三角形称为“整数三角形”．数学学习小组的同学们从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾顺次连接组成三角形，进行探究活动．如图是小亮同学用12根火柴棒，摆成如图所示的“整数三角形”．
请你分别摆出三个不同的等腰“整数三角形”，画出示意图．