
题目列表(包括答案和解析)
 =
= 。
。 

 =
= ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比。
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比。 =
= 中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明 =
= ,就可转化证
,就可转化证 =
= 。
。阅读下面材料,按要求完成后面作业.
三角形内角平分线性质定理:三角形内角平分线分对边所得的两条线段和这个角的两边对应成比例.
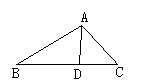
已知:△ABC中,AD是角平分线(如图).
求证:![]() =
=![]() .
.
分析:要证![]() =
=![]() ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比.
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比.
在比例式![]() =
=![]() 中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明![]() =
=![]() ,就可转化证
,就可转化证![]() =
=![]() .
.
 1.完成证明过程:
1.完成证明过程:
证明:
2.上述证明过程中,用到了哪些定理(写对两个即可)
答:用了:①
②
3.在上述分析和你的证明过程中,主要用到了下列三种数学思想的哪一种,①数形结合思想 ②转化思想 ③分类讨论思想
答:
4.用三角形内角平分线定理解答问题:
如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,B![]() D=7cm,求BD之长.
D=7cm,求BD之长.
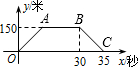 (2012•新昌县模拟)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,其中四边形OABC是等腰梯形,则下列结论中正确的是( )
(2012•新昌县模拟)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,其中四边形OABC是等腰梯形,则下列结论中正确的是( )通常,我们把长方形和正方形统称为矩形.如图1,是一个长为2a,宽为2b的矩形ABCD,若把此矩形沿图中的虚线用剪刀均分为4块小长方形,然后按照图2的形状拼成一个正方形MNPQ.
(1)分别从整体和局部的角度出发,计算图2中阴影部分的面积,可以得到等式 _________ .
(2)仔细观察长方形ABCD与正方形MNPQ,可以发现它们的 _________ 相同, _________ 不同.(选填“周长”或“面积”)
(3)根据上述发现,猜想结论:用总长为36米的篱笆围成一个矩形养鸡场,可以有许多不同的围法.在你围的所有矩形中,面积最大的矩形的面积是 _________ 米2.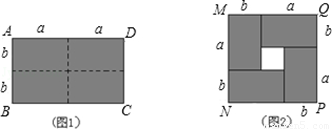
通常,我们把长方形和正方形统称为矩形.如图1,是一个长为2a,宽为2b的矩形ABCD,若把此矩形沿图中的虚线用剪刀均分为4块小长方形,然后按照图2的形状拼成一个正方形MNPQ.
(1)分别从整体和局部的角度出发,计算图2中阴影部分的面积,可以得到等式 _________ .
(2)仔细观察长方形ABCD与正方形MNPQ,可以发现它们的 _________ 相同, _________ 不同.(选填“周长”或“面积”)
(3)根据上述发现,猜想结论:用总长为36米的篱笆围成一个矩形养鸡场,可以有许多不同的围法.在你围的所有矩形中,面积最大的矩形的面积是 _________ 米2.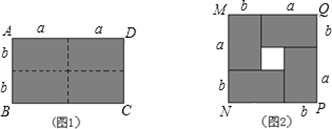
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com