
题目列表(包括答案和解析)
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。
(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是 (用含
的值是 (用含 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。
(3)拓展迁移
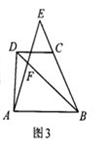
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,则
,则 的值是 (用含
的值是 (用含 的代数式表示).
的代数式表示).
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。

(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,  的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是
(用含
的值是
(用含 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。

(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,则
,则 的值是
(用含
的值是
(用含 的代数式表示).
的代数式表示).

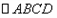 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若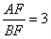 ,求
,求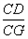 的值。
的值。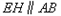 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,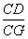 的值是
的值是 
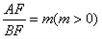 则
则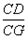 的值是 (用含
的值是 (用含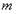 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。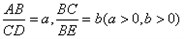 ,则
,则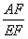 的值是 (用含
的值是 (用含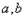 的代数式表示).
的代数式表示). 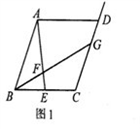

类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在![]() 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若![]() ,求
,求![]() 的值。
的值。
(1)尝试探究
在图1中,过点E作![]() 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,![]() 的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若![]() 则
则![]() 的值是 (用含
的值是 (用含![]() 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若![]() ,则
,则![]() 的值是 (用含
的值是 (用含![]() 的代数式表示).
的代数式表示).



通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。

原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线。
根据 ,易证△AFG≌ ,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com