(2013•朝阳区二模)阅读下列材料:
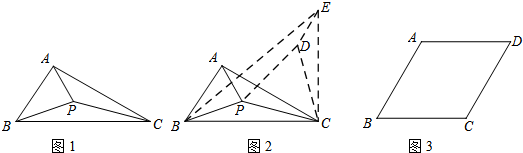
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30°,BC=6,AC=5,在△ABC内部有一点P,连接PA、PB、PC,求PA+PB+PC的最小值.
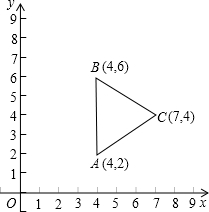
小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD、BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为
;
(2)参考小华的思考问题的方法,解决下列问题:
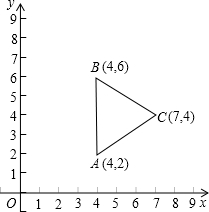
①如图3,菱形ABCD中,∠ABC=60°,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.

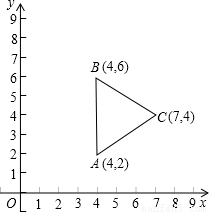
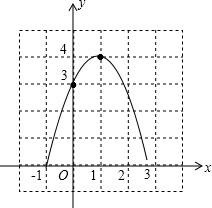 (2012•佛山)(1)任选以下三个条件中的一个,求二次函数y=ax2+bx+c的解析式;
(2012•佛山)(1)任选以下三个条件中的一个,求二次函数y=ax2+bx+c的解析式;