
题目列表(包括答案和解析)

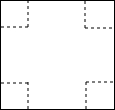 你的做法;
你的做法;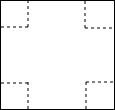 你的做法;
你的做法;问题探究.
用如图所示正方形纸板制作一个无盖的长方体盒子,可在正方体的四角减去相同的正方形,剩余部分即可做成一个无盖的长方体形盒子.
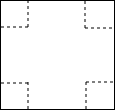
(1)设正方形纸的边长为a,减去的小正方形的边长为x,请用a与x表示这个无盖长方体形盒子的容积;
(2)把正方形的纸板换成长为a,宽为b的长方形纸板,怎样做一个无盖长方体形盒子?画图说明你的做法;
(3)把(2)中做的长方体形盒子的容积用代数式表示出来;
(4)比较(1)和(3)的结果,说说它们的区别和联系.
 “构造法”是一种重要方法,它没有固定的模式.要想用好它,需要有敏锐的观察、丰富的想象、灵活的构思.应用构造法解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行组合.
“构造法”是一种重要方法,它没有固定的模式.要想用好它,需要有敏锐的观察、丰富的想象、灵活的构思.应用构造法解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行组合.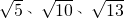 ,求这个三角形的面积.
,求这个三角形的面积.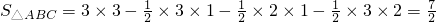
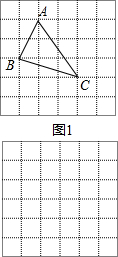
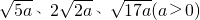 ,请在下图所示的正方形网格中(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
,请在下图所示的正方形网格中(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com