如图，是用四个全等直角三角形接成的图形，直角三角形的两条直角边分别为a、b，斜边为c，请你根据此图证明勾股定理．

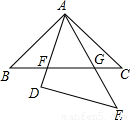
如图，已知：AB＝AD，D是BC中点，E是AD上任意一点，连接EB、EC，求证：EB＝EC．

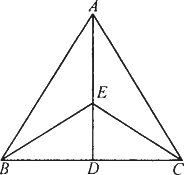
分析：(1)观察图形，图中线段EB和线段EC是________三角形中的边．现需证EB＝EC，可证△ABE≌________或△BED≌________．

(2)由已知可得BD＝CD，不要忽略图形中隐含的已知条件AE、DE、AD是三对全等三角形的公共边．

(3)找需知，只需证得∠BAE＝∠CAE或∠BDE＝∠CDE，即可得到上述两个三角形全等(恰当选择SAS来判定)．

(4)再看已知，三组对应边对应相等，可以利用SSS来证明△ABD≌△ACD，就得到∠BAE＝∠CAE或∠BDE＝∠CDE．

请同学们完成下列填空

证明一：∵D是BC中点　　∴BD＝CD

在△ABD和△ACD中，

________

________

________

∴△ABD≌△ACD(SSS)

∴∠BAE＝∠CAE(全等三角形的对应角相等)

在△ABE和△ACE中，

________

________

________

∴△ABE≌△ACE(SAS)

∴EB＝EC(全等三角形的对应边相等)

(请同学们根据分析思路，写出第二种证明方法)

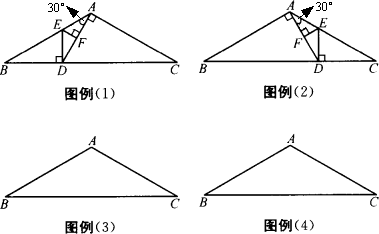
如图，已知△ABC中，∠B＝∠C＝30°，请根据图例，在图(3)和图(4)中另外设计两种不同的分法，将△ABC分割成四个三角形，使得其中两个是全等三角形，而另外两个是相似但不全等的直角三角形．

注：①画图工具不限，不要求证明，不要求写作法；

②图例(1)和图例(2)视为同一种分法；

③画出分割线段，标出分割所得三角形和顶点字母和内角度数(或记号)．