
题目列表(包括答案和解析)
在等差数列 中,若
中,若 ,则
,则 的值为( )
的值为( )
A. 6 B. 8 C. 10 D. 16
第Ⅱ卷 (非选择题 共100分)
下列四个函数图象,只有一个是符合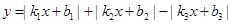 (其中
(其中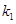 ,
,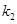 ,
,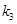 为正实数,
为正实数,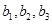 为非零实数)的图象,则根据你所判断的图象,
为非零实数)的图象,则根据你所判断的图象,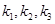 之间一定成立的关系是( )
之间一定成立的关系是( )
 |
A. 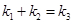 B.
B.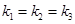 C.
C.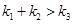 D.
D.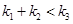
第Ⅱ卷
已知![]() 均为正数,
均为正数,![]() ,则
,则![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题中的横线上。
给出定义:若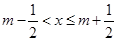 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数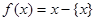 的四个命题:
的四个命题:
①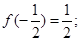 ②
②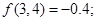
③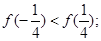 ④
④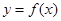 的定义域为R,值域是
的定义域为R,值域是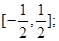
则其中真命题的序号是 ( )
A.①② B.①③ C.②④ D.③④
第Ⅱ卷
同时具有性质“①最小正周期是 ,②图像关于直线
,②图像关于直线 对称;③在
对称;③在 上是增函数”的一个函数是( )
上是增函数”的一个函数是( )
A. B.
B.

C. D.
D.
第Ⅱ卷(共110分)
一、选择题:
1―5:ACCCB 6―10:CDACD 11―12:BC
二、填空题:
13.2 14. 15.5
16.①
15.5
16.① ②球的体积函数的导数等于球的表面积函数
②球的体积函数的导数等于球的表面积函数
三、解答题:
17.(本小题满分12分)
解:(I) ……………………2分
……………………2分
 ……………………4分
……………………4分
 ……………………………………………………………………5分
……………………………………………………………………5分
(II) 、B均为锐角且B<A
、B均为锐角且B<A
又C为钝角
∴最短边为b……………………………………………………7分
由 ,解得
,解得 ………………………………9分
………………………………9分
又 …………………………12分
…………………………12分
18.(本小题满分12分)
解:(I)

 ………………………………3分
………………………………3分
故 …………………………………………………4分
…………………………………………………4分
(II)令 .
.
若 时,当
时,当 时,函数
时,函数
 …………………………………………………………6分
…………………………………………………………6分
若 时,当
时,当 时,函数
时,函数
 …………………………………………………………8分
…………………………………………………………8分
(III)由
确定 单调递增的正值区间是
单调递增的正值区间是 ;
;
由
确定 单调递减的正值区间是
单调递减的正值区间是 ;………10分
;………10分
综上,当 时,函数
时,函数 的单调递增区间为
的单调递增区间为 .
.
当 时,函数
时,函数 的单调递增区间为
的单调递增区间为 .……12分
.……12分
注:①
 的这些
的这些
等价形式中,以 最好用. 因为复合函数
最好用. 因为复合函数
 的中间变量
的中间变量 是增函数,对求
是增函数,对求 的单调区间来说,
的单调区间来说,
只看外层函数 的单调性即可.否则,利用
的单调性即可.否则,利用 的其它形
的其它形
式,例如 求单调区间是非常容易出错的. 同学们可以尝试做一
求单调区间是非常容易出错的. 同学们可以尝试做一
下 的其它形式,认真体会,比较优劣!
的其它形式,认真体会,比较优劣!
②今后遇到求类似 的单调区间问题,应首先通过诱导公式将
的单调区间问题,应首先通过诱导公式将 转化为标准形
转化为标准形
式: (其中A>0,ω>0),然后再行求
(其中A>0,ω>0),然后再行求
解,保险系数就大了.
19.(本小题满分12分)
解:(I)由已知 ……………………1分
……………………1分
 …………3分
…………3分
由已知
∴公差d=1…………………………………………………………4分

 ……………………………………………………6分
……………………………………………………6分
(II)设 …………………………7分
…………………………7分
当 时,
时, 是k的增函数,
是k的增函数, 也是k的增函数.
也是k的增函数.
 ………………………………10分
………………………………10分
又
 不存在
不存在 ,使
,使 …………………………………12分
…………………………………12分
20.(本小题满分12分)
解: 恒成立
恒成立
只需 小于
小于 的最小值…………………………………………2分
的最小值…………………………………………2分
而当 时,
时, ≥3……………………………………………4分
≥3……………………………………………4分
 ……………………………………………………6分
……………………………………………………6分
 存在极大值与极小值
存在极大值与极小值
 有两个不等的实根…………………………8分
有两个不等的实根…………………………8分

 或
或 …………………………………………………………10分
…………………………………………………………10分
要使“P且 Q”为真,只需
Q”为真,只需
故m的取值范围为[2,6].…………………………………………………12分
21.(本小题满分12分)
解:设此工厂应分别生产甲、乙两种产品x吨、y吨,获得利润z万元………1分
依题意可得约束条件:
|