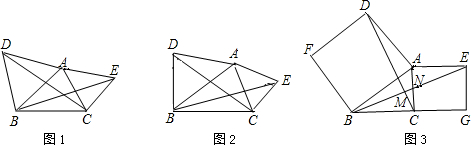
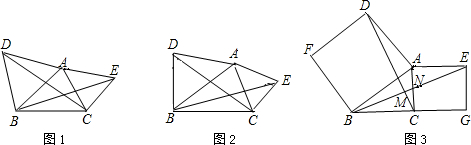
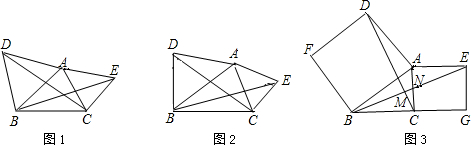
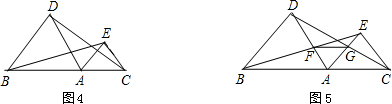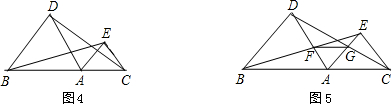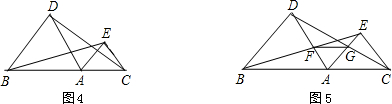题目:如图1,△ABD,△AEC都是等边三角形,求证:BE=DC.由已知易证△ABE≌△ADC,得BE=DC.
扩变:
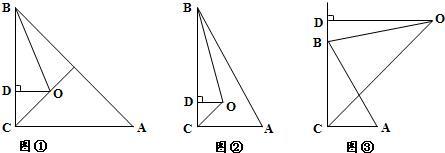
1.如图2,若△ABD,△AEC都是等腰直角三角形,∠D=∠E=90°,那么 BE=DC吗?
2.如图3,若四边形ABFD、四边形ACGE都是正方形,(1)那么 BE=DC还成立吗?(2)BE⊥DC.
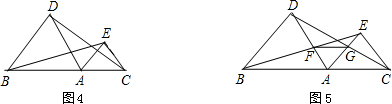
3.如图4,若点A在线段BC上,△ABD,△AEC都是等边三角形,那么BE=DC吗?
4.在3题的条件下,若AD与BE交于F点,AE与CD交于G点,如图5.
(1)AF=AG吗?
(2)△AFG是等边三角形吗?为什么?