
题目列表(包括答案和解析)
如图,抛物线经过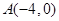 ,
, ,
,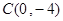 三点.
三点.
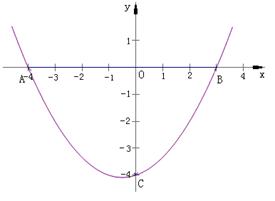
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上存在一点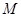 ,使
,使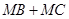 的值最小,求点
的值最小,求点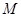 的坐标以
的坐标以
及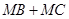 的最小值;
的最小值;
(3)在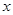 轴上取一点
轴上取一点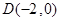 ,连接
,连接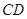 .现有一动点
.现有一动点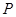 以每秒
以每秒 个单位长度的速度从点
个单位长度的速度从点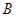 出发,沿线段
出发,沿线段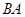 向点
向点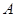 运动,运动时间为
运动,运动时间为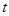 秒,另有一动点
秒,另有一动点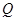 以某一速度同时从点
以某一速度同时从点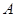 出发,沿线段
出发,沿线段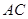 向点
向点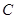 运动,当点
运动,当点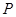 、点
、点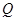 两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个
两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个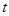 值,使线段
值,使线段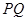 恰好被
恰好被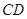 垂直平分.如果存在,请求出
垂直平分.如果存在,请求出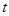 的值和点
的值和点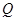 的速度,如果不存在,请说明理由.
的速度,如果不存在,请说明理由.
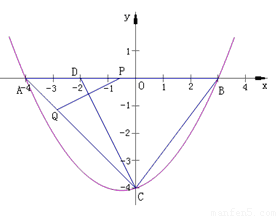
【解析】此题主要考查了用待定系数法求二次函数解析式,以及利用函数图象和图象上点的性质判断符合某一条件的点是否存在,是一道开放性题目,有利于培养同学们的发散思维能力
如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b<![]() 的解集______________;
的解集______________;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

【解析】(1)根据点A位于反比例函数的图象上,利用待定系数法求出反比例函数解析式,将点B坐标代入反比例函数解析式,求出n的值,进而求出一次函数解析式
(2)根据点A和点B的坐标及图象特点,即可求出反比例函数值大于一次函数值时x的取值范围
(3)由点A和点B的坐标求得三角形以BC 为底的高是10,从而求得三角形ABC 的面积
如图,一次函数y=kx+b与反比例函数y= 的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b< 的解集______________;
的解集______________;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

【解析】(1)根据点A位于反比例函数的图象上,利用待定系数法求出反比例函数解析式,将点B坐标代入反比例函数解析式,求出n的值,进而求出一次函数解析式
(2)根据点A和点B的坐标及图象特点,即可求出反比例函数值大于一次函数值时x的取值范围
(3)由点A和点B的坐标求得三角形以BC 为底的高是10,从而求得三角形ABC 的面积

初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com