
题目列表(包括答案和解析)
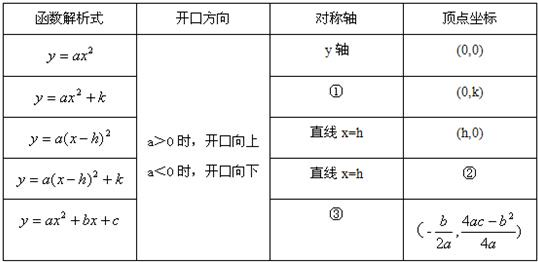

小明在学习二次函数时,总结了如下规律:
| 函数解析式 | 开口方向 | 对称轴 | 顶点坐标 |
|
| a>0时,开口向上 a<0时,开口向下 | y轴 | (0,0) |
|
| ① | (0,k) | |
|
| 直线x=h | (h,0) | |
|
| 直线x=h | ② | |
|
| ③ |
|
(1)请帮助小明补全此表① ② ③
(2)根据此表判断,如何将抛物线![]() 经过适当的平移得到抛物线
经过适当的平移得到抛物线![]() .
.

| x |
| -x |
| x |
| -x |
|
| x2-1 |
| 1-x2 |
| x-2 |
| 2-x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com