阅读材料，大数学家高斯在上学读书时

曾经研究过这样一个问题：1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+，其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…＝？

　　观察下面三个特殊的等式

　　

　　

　　

　　将这三个等式的两边相加，可以得到1×2+2×3+3×4＝

　　读完这段材料，请你思考后回答：

　　⑴　　　　　；

　　⑵1×2＋2×3＋3×4＋…＋n×(n+1)=　　　　　　　　；

　　⑶　　　　　　　。

　　（只需写出结果，不必写中间的过程）

答案

　　一、

一位同学做一道题：“已知两个多项式A、B，计算2A+B”.他误将“2A+B”看成“A+2B”，求得的结果为9 x²－2 x+7.已知B＝x²+3 x－2，求正确答案.　

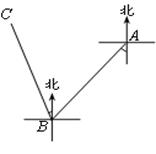
如图， 一艘轮船由海平面上A地出发向南偏西40º的方向行驶40海里到达B地，再由B地向北偏西20º的方向行驶40海里到达C地，则A、C两地相距（　　）

A．40海里    B．30海里    

C．50海里     D．60海里