
题目列表(包括答案和解析)
已知函数 (I)求
(I)求 的单调递增区间;(II)在
的单调递增区间;(II)在 中,三内角
中,三内角 的对边分别为
的对边分别为 ,已知,
,已知, 成等差数列,且
成等差数列,且 ,求
,求 的值.
的值.
已知函数 (I)求
(I)求 的单调递增区间;
的单调递增区间;
(II)在 中,三内角
中,三内角 的对边分别为
的对边分别为 ,已知
,已知 ,
, 成等差数列,且
成等差数列,且 ,求
,求 的值.
的值.
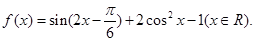 (I)求
(I)求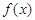 的单调递增区间;
的单调递增区间;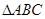 中,三内角
中,三内角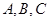 的对边分别为
的对边分别为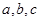 ,已知
,已知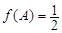 ,
,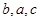 成等差数列,且
成等差数列,且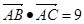 ,求
,求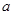 的值
的值 .
.已知函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是[-2,2]。
,单调递减区间是[-2,2]。
(I)求函数![]() 的解析式;
的解析式;
(II)若![]() 的图象与直线
的图象与直线![]() 有三个公共点,求m的取值范围。
有三个公共点,求m的取值范围。
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
D
D
C
A
C
B
A
C
二、填空题:本大题共6小题,每小题4分,共24分。把答案填在题中横线上。
11.13 12. 13.2 14.4
15.
13.2 14.4
15. 16.1005
16.1005
三、解答题:本大题共6小题,共78分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
解(I)

(Ⅱ)由 得
得 ,
,

18.(本小题满分12分)
解(I)记事件A;射手甲剩下3颗子弹,

(Ⅱ)记事件 甲命中1次10环,乙命中两次10环,事件
甲命中1次10环,乙命中两次10环,事件 ;甲命中2次10环,乙命中1次10环,则四次射击中恰有三次命中10环为事件
;甲命中2次10环,乙命中1次10环,则四次射击中恰有三次命中10环为事件

(Ⅲ) 的取值分别为16,17,18,19,20,
的取值分别为16,17,18,19,20,

 19.(本小题满分12分)
19.(本小题满分12分)
解法一:
(I)设 为
为 的中点,连结
的中点,连结 ,
,
 为
为 的中点,
的中点, 为
为 的中点,
的中点,
 ==
== ==
==
 ==
==

(Ⅱ)

(Ⅲ)过点 向
向 作垂线,垂足为
作垂线,垂足为 ,连结
,连结 ,
,

解法二:
分别以 所在直线为坐标轴建立空间直角坐标系,
所在直线为坐标轴建立空间直角坐标系,
(I)

(Ⅱ)设平面 的一个法向量为
的一个法向量为

(Ⅲ)平面 的一个法向量为
的一个法向量为

20.(本小题满分12分)
(1)由
切线的斜率 切点坐标(2,5+
切点坐标(2,5+ )
)
所求切线方程为
(2)若函数为 上单调增函数,
上单调增函数,
则 在
在 上恒成立,即不等式
上恒成立,即不等式 在
在 上恒成立
上恒成立
也即 在
在 上恒成立。
上恒成立。
令 上述问题等价于
上述问题等价于
而 为在
为在 上的减函数,
上的减函数,
则 于是
于是 为所求
为所求
21.(本小题满分14分)
解(I)设

(Ⅱ)(1)当直线 的斜率不存在时,方程为
的斜率不存在时,方程为


(2)当直线 的斜率存在时,设直线的方程为
的斜率存在时,设直线的方程为 ,
,
设 ,
,
 ,得
,得




22.(本小题满分14分)
解(I)由题意,令

(Ⅱ)

(1)当 时,
时, 成立:
成立:
(2)假设当 时命题成立,即
时命题成立,即
当 时,
时,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com