回答有关“生物体内物质变化和能量转换”问题(共21分)

Ⅰ.下图Ⅰ表示人体有氧呼吸的过程,其中①~③表示相关过程,甲、乙表示相应物质。请据图回答:

41.图Ⅰ中物质乙表示 ,过程②发生的场所称为 。
42.图Ⅰ中热能产生的意义在于 。
43.运动员短跑后会出现肌肉酸痛现象,主要原因是肌细胞中产生了乳酸,图Ⅱ中代表乳酸浓度变化的曲线是 。现代健身提倡进行有氧运动,请举出一个具体的例子并说明此运动类型的优点:
。
Ⅱ.回答下列关于光合作用的系列问题。
44.在植物光合作用过程中,光反应中能把光能转换成电能的叶绿素是少数处于特殊状态的?? 。温度主要影响光合作用的阶段。光反应阶段产生的[H]和ATP用于

暗反应中 45.下表为某同学探究影响植物光合作用因素所做的实验。据图表可知,探究的影响因素有 。要比较不同颜色的光对光合作用的影响,应选择的容器标

号是 。
容器
| 植物
| 部位
| 光质
| 温度(℃)
| O2增加量(mL/8小时)
|
1
| 天竺葵
| 叶
| 红
| 22
| 120
|
2
| 天竺 葵 葵
| 叶
| 黄
| 22
| 15
|
3
| 天竺葵
| 根
| 红
| 22
| -10
|
4
| 紫罗兰
| 叶
| 红
| 22
| 80
|
5
| 紫罗兰
| 叶
| 黄
| 22
| 10
|
46.用鸭茅大小相似的绿色叶片,放在特定的实验装置中。研究在10℃、20℃的温度下,分别置于5000 lx,20000 lx光照和黑暗条件下的光合作用和呼吸作用。结果如下图所示。

该叶片在20℃下呼吸速率是10℃下的___________倍。该叶片在10℃、5000 lx的光照条件下,每小时光合作用所产生的氧气量是_______mg。该叶片在 20℃、20000lx的光照条件下,如果光合作用合成的有机物都是葡萄糖,每小时产生的葡萄糖为____________mg。
III.下图示淀粉、脂肪、蛋白质被人体摄入后的氧化分解代谢变化关系模式图。图中字母A、B、C、D、E、F表示某些分子、原子或基团,X代表某细胞器,数字表示相应生理过程。
47.请写出下列物质或生理过程的名称:
B ; F ;② ;③ 。
48.产生ATP最多的是过程 m]
49.写出有氧呼吸的总反应式 。

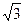 )2+(π一3.14) 0一(2+
)2+(π一3.14) 0一(2+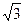 )-1;
)-1; )2+(π一3.14) 0一(2+
)2+(π一3.14) 0一(2+ )-1;
)-1;

 暗反应中 45.下表为某同学探究影响植物光合作用因素所做的实验。据图表可知,探究的影响因素有 。要比较不同颜色的光对光合作用的影响,应选择的容器标
暗反应中 45.下表为某同学探究影响植物光合作用因素所做的实验。据图表可知,探究的影响因素有 。要比较不同颜色的光对光合作用的影响,应选择的容器标 号是 。
号是 。 葵
葵
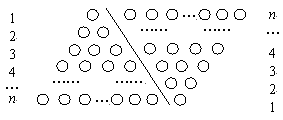
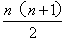 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=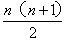 。
。
 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n= .
.