如图，现有图1所示的长方形纸板360张和正方形纸板140张，制作图2所示的A，B两种长方体形状的无盖纸盒，刚好全部用完．问能制作A型盒子、B型盒子各多少个？若设能做成x个A型盒子，y个B型盒子，则依题意可列出方程组

x+2y=140 4x+3y=360

．如果设做A型盒子用了正方形纸板x张，做B型盒子用了正方形纸板y张，则以下列出的方程组中正确的为（　　）

（2013•河东区一模）请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个长方体形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点．若广告商要求包装盒侧面积Scm²最大，试求x应取何值？
设AE=FB=xcm，包装盒侧面积为Scm²．

（I）分析：由正方形硬纸片ABCD的边长为60cm，AE=FB=xcm，则EF=cm．
为更好地寻找题目中的等量关系，将剪掉的阴影部分三角形集中，得到边长为EF的正方形，其面积为cm²；折起的四个角上的四个等腰直角三角形的面积之和为cm²．
（Ⅱ）由以上分析，用含x的代数式表示包装盒的侧面积S，并求出问题的解．

堆放在地面上垒成长方体形状的一堆砖，长为30块砖，宽为20块砖，高为10块砖，给这堆砖露出的表面普遍洒上石灰水，则没有洒上石灰水的砖的块数是（　　）

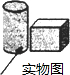（2012•道里区一模）在水平的讲台上放置圆柱形状的水杯和长方体形状的粉笔盒，如实物图，则此实物图的 左视图是（　　）

（2013•吉林）某校数学课题学习小组在“测量教学楼高度”的活动中，设计了以下两种方案：

课题	测量教学楼高度
方案	一	二
图示
测得数据	CD=6.9m，∠ACG=22°，∠BCG=13°，	EF=10m，∠AEB=32°，∠AFB=43°
参考数据	sin22°≈0.37，cos22°≈0.93， tan22°≈0.40 sin13°≈0.22，cos13°≈0.97 tan13°≈0.23	sin32°≈0.53，cos32°≈0.85，tan32°≈0.62 sin43°≈0.68，cos43°≈0.73，tan43°≈0.93

请你选择其中的一种方法，求教学楼的高度（结果保留整数）