
题目列表(包括答案和解析)
已知函数![]() 的最大值为正实数,集合
的最大值为正实数,集合
![]() ,集合
,集合![]() 。
。
(1)求![]() 和
和![]() ;
;
(2)定义![]() 与
与![]() 的差集:
的差集:![]() 且
且![]() 。
。
设![]() ,
,![]() ,
,![]() 均为整数,且
均为整数,且![]() 。
。![]() 为
为![]() 取自
取自![]() 的概率,
的概率,![]() 为
为![]() 取自
取自![]() 的概率,写出
的概率,写出![]() 与
与![]() 的二组值,使
的二组值,使![]() ,
,![]() 。
。
(3)若函数![]() 中,
中,![]() ,
,![]() 是(2)中
是(2)中![]() 较大的一组,试写出
较大的一组,试写出![]() 在区间[
在区间[![]() ,n]上高考资源网的最 大值函数
,n]上高考资源网的最 大值函数![]() 的表达式。
的表达式。
若函数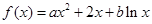 在
在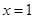 和
和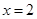 处取得极值,
处取得极值,
(1)求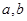 的值;
的值;
(2)求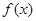 在
在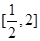 上的最大值和最小值.
上的最大值和最小值.
若函数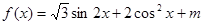 在区间
在区间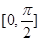 上的最小值为3,
上的最小值为3,
(1)求常数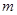 的值;
的值;
(2)求此函数当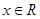 时的最大值和最小值,并求相应的
时的最大值和最小值,并求相应的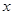 的取值集合。
的取值集合。
 在
在 和
和 处取得极值,
处取得极值, 的值;
的值; 在
在 上的最大值和最小值.
上的最大值和最小值.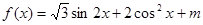 在区间
在区间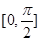 上的最小值为3,
上的最小值为3,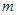 的值;
的值;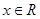 时的最大值和最小值,并求相应的
时的最大值和最小值,并求相应的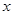 的取值集合。
的取值集合。ABCACDCCDB
 2
2 

(2,1)È(1,2) -2
17、解:(Ⅰ)

(Ⅱ)

 18、[解](1)
18、[解](1)
(2)方程 的解分别是
的解分别是 和
和 ,由于
,由于 在
在 和
和 上单调递减,在
上单调递减,在 和
和 上单调递增,因此
上单调递增,因此
 .
.
由于 .
.
19、解:(Ⅰ)

 ①
①
由方程 ②
②
因为方程②有两个相等的根,所以 ,
,
即 
由于 代入①得
代入①得 的解析式
的解析式

(Ⅱ)由
及
由 解得
解得 
故当 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是
20、解:(Ⅰ)设函数 的图象上任意一点
的图象上任意一点 关于原点的对称点为
关于原点的对称点为 ,则
,则

∵点 在函数
在函数 的图象上
的图象上
∴
(Ⅱ)由
当 时,
时, ,此时不等式无解
,此时不等式无解
当 时,
时, ,解得
,解得

因此,原不等式的解集为

21、解: (Ⅰ)由原式得
∴
(Ⅱ)由 得
得 ,此时有
,此时有 .
.
由 得
得 或x=-1 , 又
或x=-1 , 又
所以f(x)在[--2,2]上的最大值为 最小值为
最小值为
(Ⅲ)解法一:  的图象为开口向上且过点(0,--4)的抛物线,由条件得
的图象为开口向上且过点(0,--4)的抛物线,由条件得

即 ∴--2≤a≤2.
∴--2≤a≤2.
所以a的取值范围为[--2,2].
解法二:令 即
即 由求根公式得:
由求根公式得: 
所以 在
在 和
和 上非负.
上非负.
由题意可知,当x≤-2或x≥2时,  ≥0,
≥0,
从而x1≥-2, x2≤2,
即 解不等式组得: --2≤a≤2.
解不等式组得: --2≤a≤2.
∴a的取值范围是[--2,2].
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com