函数y=㏒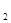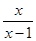(x﹥1)的反函数是

A.y=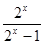 (x>0)  B.y= 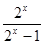(x<0)  C.y= 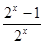(x>0)  D. .y= 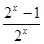(x<0)

在平面直角坐标系xOy中,设定点A(a,a),P是函数y=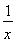(x>0)图象上一动点.若点P,A之间的最短距离为2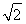,则满足条件的实数a的所有值为　　　　. 

a>0且a≠1，x>y>0时，判断下列式子是否正确．

(1)logax·logay＝loga(x＋y)；

(2)logax－logay＝loga(x－y)；

(3)loga＝logax÷logay；

(4)logaxy＝logax－logay；

(5)(logax)n＝nlogax；

(6)logax＝－loga；

(7)＝logax.

[分析]　根据对数的运算律加以判断即可．

已知函数f(x)＝alnx－x²＋1.

(1)若曲线y＝f(x)在x＝1处的切线方程为4x－y＋b＝0，求实数a和b的值；

(2)若a<0，且对任意x₁、x₂∈(0，＋∞)，都|f(x₁)－f(x₂)|≥|x₁－x₂|，求a的取值范围．

【解析】第一问中利用f′(x)＝－2x(x>0)，f′(1)＝a－2，又f(1)＝0，所以曲线y＝f(x)在x＝1处的切线方程为y＝(a－2)(x－1)，即(a－2)x－y＋2－a＝0，

由已知得a－2＝4,2－a＝b，所以a＝6，b＝－4.

第二问中，利用当a<0时，f′(x)<0，∴f(x)在(0，＋∞)上是减函数，

不妨设0<x₁≤x₂，则|f(x₁)－f(x₂)|＝f(x₁)－f(x₂)，|x₁－x₂|＝x₂－x₁，

∴|f(x₁)－f(x₂)|≥|x₁－x₂|等价于f(x₁)－f(x₂)≥x₂－x₁，

即f(x₁)＋x₁≥f(x₂)＋x₂，结合构造函数和导数的知识来解得。

(1)f′(x)＝－2x(x>0)，f′(1)＝a－2，又f(1)＝0，所以曲线y＝f(x)在x＝1处的切线方程为y＝(a－2)(x－1)，即(a－2)x－y＋2－a＝0，

由已知得a－2＝4,2－a＝b，所以a＝6，b＝－4.

(2)当a<0时，f′(x)<0，∴f(x)在(0，＋∞)上是减函数，

不妨设0<x₁≤x₂，则|f(x₁)－f(x₂)|＝f(x₁)－f(x₂)，|x₁－x₂|＝x₂－x₁，

∴|f(x₁)－f(x₂)|≥|x₁－x₂|等价于f(x₁)－f(x₂)≥x₂－x₁，即f(x₁)＋x₁≥f(x₂)＋x₂，

令g(x)＝f(x)＋x＝alnx－x²＋x＋1，g(x)在(0，＋∞)上是减函数，

∵g′(x)＝－2x＋1＝(x>0)，

∴－2x²＋x＋a≤0在x>0时恒成立，

∴1＋8a≤0，a≤－，又a<0，

∴a的取值范围是

已知函数f(x)=xlnx² (x<-1)的导函数为g(x)，则g(x)的反函数是               （    ）

A．y=(x<2)     B．y=(x>2)            C．y=-(x>2)           D．y=-(x<2)