题目列表(包括答案和解析)
（本小题满分12分）
设函数
是定义域为R上的奇函数；
（Ⅰ）若
，试求不等式
的解集；
（Ⅱ）若
上的最小值。
（本小题满分12分）
设函数
是定义域为R上的奇函数。
（1）若
的解集；
（2）若
上的最小值为—2，求m的值。
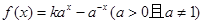是定义域为R上的奇函数；
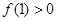，试求不等式
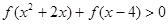的解集；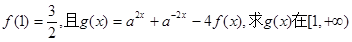
上的最小值。（本小题满分12分）设函数
若它是R上的单调函数，且1是它的零点。
（1）求实数a的值；
|
的图象的切线与x轴交于点
的图象的切线与x轴于
……，依此下去，过
作函数
的图象的切线与x轴交于点
……，若
求证：
成等比数列；并求数列
的通项公式
。（已知
）（本小题满分12分）设函数f（x）的定义域是R，对于任意实数m,n，恒有f（m+n）=f（m）f（n），且当x>0时，0<f（x）<1。
（1）求证：f（0）=1，且当x<0时，有f（x）>1；
（2）判断f（x）在R上的单调性；
⑶设集合A＝{（x,y）|f（x2）f（y2）>f（1）}，集合B＝{（x,y）|f（ax－y+2）=1,a∈R}，若A∩B＝
，求a的取值范围。
一、1. [0,2]
2. 2≤x<5或x>5
3. 4 4. 
5. 720 6. 
7. x(1－x)
8.(文) 2 (理) 
9. 10. 
11. ①②④ 12. 0
二、13. A 14. D 15. A 16.C
三、
17. 解：（1）
上的奇函数，
即
。
（2）由（1）得：
，即
，
。
18. 解：
有两个不等的负根，
…………3分
无实根，
得
……6分
有且只有一个为真，若p真q假，得
………………9分
若p假q真，得
………………11分
综合上述得
……………………12分
19．f(x)在(－∞,－1)上是增函数, f(x)在(－1,0)上是减函数。 ………………4分
证明：任取x1,x2，使x1<x2<0,则
………………7分
∵ x1<x2<0，x2－x1>0 x1?x2>0, 当x1<x2<－1时
∴ 
即 
∴ f(x)在(－∞,－1)上是增函数。 ………………10分
当－1<x1<x2<0时
f(x2)－f(x1)<0,即f(x2)<f(x1)
∴ f(x)在(－1,0)上是减函数。 ………………12分
20. 解：（1）当a＝2时，A＝（2，7），B＝（4，5）∴ A
B＝（4，5）.………4分
（2）∵ B＝（
时，A＝（
要使B
A，必须
，此时a＝－1；…………………………………7分
当a＝时，A＝
，使BA的a不存在； ……………………………………8分
当a＞时，A＝（2，
要使BA，必须
，此时1≤a≤3. ………………………………11分综上可知，使BA的实数a的取值范围为[1，3]∪{－1}………………………12分
21、解：解：据题意，商品的价格随时间
变化，且在不同的区间
与
上，价格随时间
的变化的关系式也不同，故应分类讨论
设日销售额为
⑴当
时，
。 ………………3分
所以，当
或11时，
。
………6分
⑵当
时，
…9分
所以，当
时，
。
…11分
综合（1）、（2）知当或11时，日销售额最大，最大值为176。…………12分
22、解：（1）显然函数
的值域为
； ……………4分
（2）若函数
在定义域上是减函数，
则任取
且
都有
成立，
即
只要
即可，
由
，故
，所以
，
故
的取值范围是
； ……………9分
（3）当
时，函数
在
上单调增，无最小值，
当
时取得最大值
；
由（2）得当
时，函数
在
上单调减，无最大值，
当
时取得最小值
；
当
时，函数
在
上单调减，在
上单调增，无最大值，
……………13分
当
时取得最小值
. ……………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com