练习册

  • 练习册
  • 试题
    21．根据市场调查.某商品在最近的40天内的价格f(t)与时间满足关系销售量g(t)与时间t满足关系求这种商品的日销售额的最大值 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）

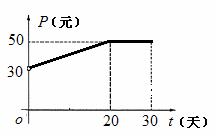
    根据市场调查，某种新产品投放市场的30天内，每件销售价格P（元）与时间t（天 ）的关系满足下图，日销量Q（件）与时间t（天）之间的关系是．

       （Ⅰ）写出该产品每件销售价格P与时间t的函数关系式；

    （Ⅱ）在这30天内，哪一天的日销售金额最大？

    （日销量金额=每件产品销售价格×日销量）

    查看答案和解析>>

    （本小题满分12分）某商场以100元/件的价格购进一批衬衣，以高于进价的价格出售，销售有淡季旺季之分.通过市场调查发现：①销售量（件）与衬衣标价x（元/件）在销售旺季近似地符合函数关系：；在销售淡季近似地符合函数关系：、、、为常数；②在销售旺季，商场以140元/件的价格销售能获得最大销售利润；③若称①中时的标价x为衬衣的“临界价格”，则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.

    请根据上述信息，完成下面问题：

       （Ⅰ）填出表格中空格的内容；

    数量关系

    销售季节

    标价

    （元/件）

    销售量（件）

    （含k、b1或b­2）

    不同季节的销售总利润y（元）

    与标价x（元/件）的函数关系式

    旺  季

    x

    淡  季

    x

       （Ⅱ）在销售淡季，该商场要获得最大销售利润，衬衣的标价应定为多少元才合适？

    查看答案和解析>>

    （本小题满分12分）某工厂生产某种儿童玩具，每件玩具的成本为30元，并且每件玩具的加工费为元（其中为常数，且），设该工厂每件玩具的出厂价为元（），根据市场调查，日销售量与（为自然对数的底数）成反比例，当每件玩具的出厂价为40元时，日销售量为10件.

    （Ⅰ）求该工厂的日利润(元)与每件玩具的出厂价元的函数关系式；

    （Ⅱ）当每件玩具的日售价为多少元时，该工厂的利润最大，并求的最大值.

    查看答案和解析>>

    （本小题满分12分）

    某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2，

    （注：利润与投资单位是万元）

    （1）分别将A，B两种产品的利润表示为投资的函数，并写出它们的函数关系式.（2）该企业已筹集到10万元资金，并全部投入到A，B两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大利润为多少万元.

    查看答案和解析>>

    （本小题满分12分）某商场以100元/件的价格购进一批衬衣，以高于进价的价格出售，销售有淡季旺季之分.通过市场调查发现：①销售量（件）与衬衣标价x（元/件）在销售旺季近似地符合函数关系：；在销售淡季近似地符合函数关系：、、、为常数；②在销售旺季，商场以140元/件的价格销售能获得最大销售利润；③若称①中时的标价x为衬衣的“临界价格”，则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.

    请根据上述信息，完成下面问题：

       （Ⅰ）填出表格中空格的内容；

    数量关系

    销售季节

    标价

    （元/件）

    销售量（件）

    （含k、b1或b­2）

    不同季节的销售总利润y（元）

    与标价x（元/件）的函数关系式

    旺  季

    x

    淡  季

    x

       （Ⅱ）在销售淡季，该商场要获得最大销售利润，衬衣的标价应定为多少元才合适？

    查看答案和解析>>

    一、1. [0,2]  2. 2≤x<5或x>5  3. 4   4.   5. 720  6.   7. x(1－x)

    8.(文) 2 (理)   9.  10.  11. ①②④  12. 0

    二、13. A  14. D  15. A   16.C      

    三、

    17. 解：（1）上的奇函数，即。

    （2）由（1）得：，即，

    。

     

    18. 解：有两个不等的负根，   …………3分

    无实根，得 ……6分

    有且只有一个为真，若p真q假，得                   ………………9分

    若p假q真，得                                ………………11分

    综合上述得                        ……………………12分

    19．f(x)在(－∞,－1)上是增函数, f(x)在(－1,0)上是减函数。      ………………4分

    证明：任取x1,x2，使x1<x2<0,则

                                    ………………7分

           ∵    x1<x2<0，x2－x1>0     x1?x2>0, 当x1<x2<－1时

           ∴   

           即   

           ∴    f(x)在(－∞,－1)上是增函数。                        ………………10分

       当－1<x1<x2<0时

    f(x2)－f(x1)<0,即f(x2)<f(x1)

    ∴   f(x)在(－1,0)上是减函数。                           ………………12分

    20. 解：（1）当a＝2时，A＝（2，7），B＝（4，5）∴ AB＝（4，5）.………4分

    （2）∵ B＝（2a，a2＋1），当a＜时，A＝（3a＋1，2）        ……………5分

    要使BA，必须，此时a＝－1；…………………………………7分

    当a＝时，A＝，使BA的a不存在； ……………………………………8分

    当a＞时，A＝（2，3a＋1）                             ………………9分

    要使BA，必须，此时1≤a≤3.    ………………………………11分综上可知，使BA的实数a的取值范围为[1，3]∪{－1}………………………12分

    21、解：解：据题意，商品的价格随时间变化，且在不同的区间与上，价格随时间的变化的关系式也不同，故应分类讨论

    设日销售额为

    ⑴当时，

    。  ………………3分

    所以，当或11时，。                          ………6分

    ⑵当时，    …9分

    所以，当时，。                                   …11分

    综合（1）、（2）知当或11时，日销售额最大，最大值为176。…………12分

    22、解：（1）显然函数的值域为；         ……………4分

    （2）若函数在定义域上是减函数，

    则任取且都有 成立，

       即只要即可，        

    由，故，所以，

    故的取值范围是；                              ……………9分

    （3）当时，函数在上单调增，无最小值，

     当时取得最大值；

    由（2）得当时，函数在上单调减，无最大值，

    当时取得最小值；

     当时，函数在上单调减，在上单调增，无最大值，                                                        ……………13分

        当 时取得最小值.                        ……………14分

     


    同步练习册答案