
题目列表(包括答案和解析)
(本题满分5分)如图,小明在大楼30米高
(即PH=30米)的窗口P处进行观测,测得山
坡上A处的俯角为15°,山脚B处的俯角为
60°,已知该山坡的坡度i(即tan∠ABC)为1:
 ,点P、H、B、C、A在同一个平面上.点
,点P、H、B、C、A在同一个平面上.点
H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 ▲ 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ≈1.732).
≈1.732).
丽水市在规划新城期间,欲拆除瓯江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)

如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: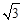 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
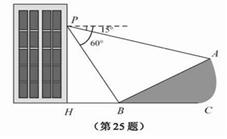
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: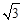 ≈1.732).
≈1.732).
请同学们认真阅读下面材料,然后解答问题。(6分)
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±
当y=4时,有x2-1=4,即x2=5 ∴x=±
∴原方程的解为:x1=- x2=
x2= x3=-
x3=- x4=
x4=
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程 -3(
-3( -3)=0
-3)=0
某农户计划利用现有的一面墙(墙长8米),再修四面墙,建造如图所示的长方体水池,培育不同品种的鱼苗.他已备足可以修高为1.5m、长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度).
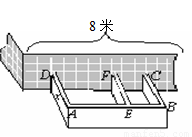
(1)若想水池的总容积为36m3,x应等于多少?
(2)求水池的总容积V与x的函数关系式,并直接写出x的取值范围;
(3)若想使水池的总容积V最大,x应为多少?最大容积是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com