
题目列表(包括答案和解析)
已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当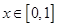 时,
时,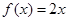 ,且在
,且在 内,关于
内,关于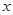 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是
已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,且在
,且在 内,关于
内,关于 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是
 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,且在
,且在 内,关于
内,关于 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是 (08年扬州中学) 已知![]() 是以2为周期的偶函数,当
是以2为周期的偶函数,当![]() 时,
时,![]() ,且在
,且在![]() 内,关于
内,关于![]() 的方程
的方程![]() 有四个根,则
有四个根,则![]() 得取值范围是
得取值范围是
 ;
; 恒成立,则a的取值范围是
恒成立,则a的取值范围是 ;
; 上没有实数根,则k的取值范围是k≥2;
上没有实数根,则k的取值范围是k≥2;一、填空题
1、 2、
2、 3、(1)(2)(3)(4) 4、
3、(1)(2)(3)(4) 4、 5、
5、 6、3
6、3
7、 8、
8、 9、
9、 10、不能 11、
10、不能 11、 12、46 13、
12、46 13、
14、(3)(4)
二、解答题
15、解:(1)sin3α=sin(2α+α)=sin2αcosα+cos2αsinα
=2sinαcos2α+(1-2sin2α)sinα
=2sinα(1-sin2α)+(1-2sin2α)sinα=3sinα-4sin3α .
(2)∵sin54°=cos36°,
∴3sin18°-4sin318°=1-2sin18°.
令t= sin18°,则上式可变形为3t-4t3=1-2t2,即
(t-1)(4t2+2t-1)=0.
解得  (t= 1与
(t= 1与 均不合,舍去).
均不合,舍去).
∴sin18°= .
.
16、证明:(1)连结 ,在
,在 中,
中, 、
、 分别为
分别为 ,
, 的中点,则
的中点,则


(2)





3)
 且
且 
 ,
,

∴ 即
即
 =
=
=
17、解:由已知圆的方程为 ,
,
按 平移得到
平移得到 .
.
∵ ∴
∴ .
.
即 .
.
又 ,且
,且 ,∴
,∴ .∴
.∴ .
.
设 ,
,
 的中点为D.
的中点为D.
由 ,则
,则 ,又
,又 .
.
∴ 到
到 的距离等于
的距离等于 .
.
即 , ∴
, ∴ .
.
∴直线 的方程为:
的方程为: 或
或 .
.
18、解:(1)如下图

(2) =3
=3 2.5+4
2.5+4 3+5
3+5 4+6
4+6 4.5=66.5
4.5=66.5
 =
= =4.5
=4.5
 =
= =3.5
=3.5



故线性回归方程为y=0.7x+0.35
(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为0.7 100+0.35=70.35
100+0.35=70.35
故耗能减少了90-70.35=19.65(吨)
19、解:(1)由
 是首项为
是首项为 ,公比为
,公比为 的等比数列
的等比数列
当 时,
时, ,
,
所以

(2)由 得
得
 (作差证明)
(作差证明)

综上所述当 时,不等式
时,不等式 对任意
对任意 都成立.
都成立.
20.解:(1) ,由题意及导数的几何意义得
,由题意及导数的几何意义得
 ,
, (1)
(1)
 ,
(2)
,
(2)
又 ,可得
,可得 ,即
,即 ,故
,故
由(1)得 ,代入
,代入 ,再由
,再由 ,得
,得
 ,
(3)
,
(3)
将 代入(2)得
代入(2)得 ,即方程
,即方程 有实根.
有实根.
故其判别式 得
得
 ,或
,或 ,
(4)
,
(4)
由(3),(4)得 ;
;
(2)由 的判别式
的判别式 ,
,
知方程 有两个不等实根,设为
有两个不等实根,设为 ,
,
又由 知,
知, 为方程(
为方程( )的一个实根,则有根与系数的关系得
)的一个实根,则有根与系数的关系得
 ,
,
当 或
或 时,
时, ,当
,当 时,
时, ,
,
故函数 的递增区间为
的递增区间为 ,由题设知
,由题设知 ,
,
因此 ,由(Ⅰ)知
,由(Ⅰ)知 得
得
 的取值范围为
的取值范围为 ;
;
(3)由 ,即
,即 ,即
,即 ,
,
因为 ,则
,则 ,整理得
,整理得 ,
,
设 ,可以看作是关于
,可以看作是关于 的一次函数,
的一次函数,
由题意 对于
对于 恒成立,
恒成立,
故 即
即 得
得 或
或 ,
,
由题意, ,
,
故 ,因此
,因此 的最小值为
的最小值为 .
.
理科加试题:
1、(1)“油罐被引爆”的事件为事件A,其对立事件为 ,则P(
,则P( )=C
)=C
∴P(A)=1- 答:油罐被引爆的概率为
答:油罐被引爆的概率为
(2)射击次数ξ的可能取值为2,3,4,5,
P(ξ=2)= , P(ξ=3)=C
, P(ξ=3)=C ,
,
P(ξ=4)=C , P(ξ=5)=C
, P(ξ=5)=C
ξ
2
3
4
5




故ξ的分布列为:
Eξ=2× +3×
+3× +4×
+4× +5×
+5× =
=
2、解:(1)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则 ,
,
∴函数f(x)的解析式为
(2)由 得
得
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(
由定积分的几何意义知:



选做
1、解:(1)证明:连结 .
.
因为 与圆
与圆 相切于点
相切于点 ,所以
,所以 .
.
因为 是圆
是圆 的弦
的弦 的中点,所以
的中点,所以 .
.
于是 .
.
由圆心 在
在 的内部,可知四边形
的内部,可知四边形 的对角互补,所以
的对角互补,所以 四点共圆.
四点共圆.
(2)解:由(Ⅰ)得 四点共圆,所以
四点共圆,所以 .
.
由(Ⅰ)得 .
.
由圆心 在
在 的内部,可知
的内部,可知 .
.
所以 .
.
2、解:在矩阵N=
 的作用下,一个图形变换为其绕原点逆时针旋转
的作用下,一个图形变换为其绕原点逆时针旋转 得到的图形,在矩阵M=
得到的图形,在矩阵M=
 的作用下,一个图形变换为与之关于直线
的作用下,一个图形变换为与之关于直线 对称的图形。因此
对称的图形。因此
△ABC在矩阵MN作用下变换所得到的图形与△ABC全等,从而其面积即为1
3、解:以极点为原点,极轴为 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1) ,
, ,由
,由 得
得 .
.
所以 .
.
即 为
为 的直角坐标方程.
的直角坐标方程.
同理 为
为 的直角坐标方程.
的直角坐标方程.
(2)由
 解得
解得
 .
.
即 ,
, 交于点
交于点 和
和 .过交点的直线的直角坐标方程为
.过交点的直线的直角坐标方程为 .
.
 4、解:
4、解:
(1)令 ,则
,则
 ...............3分
...............3分
作出函数 的图象,它与直线
的图象,它与直线 的交点为
的交点为 和
和 .
.
所以 的解集为
的解集为 .
.
(2)由函数 的图像可知,当
的图像可知,当 时,
时, 取得最小值
取得最小值 .
.
等于△ABC的面积,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com