
题目列表(包括答案和解析)
当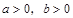 时,有以下四个不等式:①
时,有以下四个不等式:①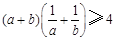 ;
②
;
②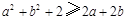 ;
;
③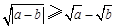 ; ④
; ④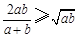 .
.
其中不等式恒成立的是 .(填出所有正确答案的序号)
 ),x∈[4,8]时的图象,图象的最高点为
),x∈[4,8]时的图象,图象的最高点为

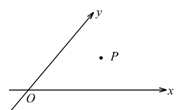
如图,设 ,且
,且 .当
.当 时,定义平面坐标系
时,定义平面坐标系 为
为 -仿射坐标系,在
-仿射坐标系,在 -仿射坐标系中,任意一点
-仿射坐标系中,任意一点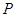 的斜坐标这样定义:
的斜坐标这样定义: 分别为与
分别为与 轴、
轴、 轴正向相同的单位向量,若
轴正向相同的单位向量,若 ,则记为
,则记为 ,那么在以下的结论中,正确的有.(填上所有正确结论的序号)
,那么在以下的结论中,正确的有.(填上所有正确结论的序号)
①设 、
、 ,若
,若 ,则
,则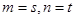 ;
;
②设 ,则
,则 ;
;
③设 、
、 ,若
,若 ,则
,则 ;
;
④设 、
、 ,若
,若 ,则
,则 ;
;
⑤设 、
、 ,若
,若 与
与 的夹角
的夹角 ,则
,则 .
.
 ),x∈[4,8]时的图象,图象的最高点为
),x∈[4,8]时的图象,图象的最高点为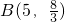

设函数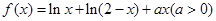 .
.
(Ⅰ) 当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
【解析】第一问中利用函数 的定义域为(0,2),
的定义域为(0,2), .
.
当a=1时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
第二问中,利用当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
解:函数 的定义域为(0,2),
的定义域为(0,2), .
.
(1)当 时,
时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
(2)当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com