题目列表(包括答案和解析)
（09年湖北百所重点联考理）（12分）设A是符合以下性质的函数
且
上是减函数。
（1）判断函数
是否属于集合A，并简要说明理由；
对任意的
总成立，求实数k的取值范围。设A是同时符合以下性质的函数
组成的集合：
①
，都有
；②在
上是减函数．
（1）判断函数
和
(x≥0)是否属于集合A，并简要说明理由；
（2）把（1）中你认为是集合A中的一个函数记为
,若不等式
≤k对任意的x≥0总成立，求实数
的取值范围．
集合A是由具备下列性质的函数
组成的：
① 函数的定义域是
；
② 函数的值域是
；
③ 函数在上是增函数，试分别探究下列两小题：
（1）判断函数
及
是否属于集合A？
并简要说明理由；
（2）对于（1）中你认为属于集合A的函数，不等式
是否对于任意的
恒成立？若成立，请给出证明；若不成立，请说明理由.
集合A是由具备下列性质的函数
组成的：
(1) 函数的定义域是
；
(2) 函数的值域是
；
(3) 函数在上是增函数．试分别探究下列两小题：
（Ⅰ）判断函数
，及
是否属于集合A？并简要说明理由．
（Ⅱ）对于（I）中你认为属于集合A的函数，不等式
，是否对于任意的
总成立？若不成立，为什么？若成立，请证明你的结论．
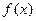组成的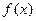：的定义域是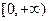
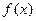； 的值域是
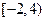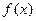；在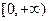上是增函数．试分别探究下列两小题：
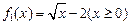，及
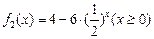是否属于集合A？并简要说明理由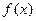．，不等式
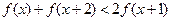，是否对于任意的
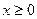总成立？若不成立，为什么？若成立，请证明你的结论．
1．D 2．B 3．D 4．B 5．A 6．B 7．C 8．B 9．A 10．C
11．
12．
13．3 14．
15．①②④
16．解：（1）由题意，得
………………2分
解不等式组，得
……4分
（2）
………………6分
………………7分
上是增函数。 ………………10分
又
，
………………12分
17．解：（1）
，
不在集合A中。 ………………3分
又
， ………………5分
上是减函数，
在集合A中。 ………………8分
（2）当
， ………………11分
又由已知
，
因此所求的实数k的取值范围是
………………12分
18．解：（1）当
定义域为
………………7分
（2）对于
，
显然当
（元）， ………………9分
∴当每辆自行车的日租金定在11元时，才能使一日的净收入最多。…………12分
19．解：（1）选取的5只恰好组成完整“奥运吉祥物”的概率
ξ的分布列为
ξ
100
80
60
40
P
………………11分
………………13分
20．解：（1）
恒成立，
知
从而
………………4分
（2）由（1）可知
，
由于
是单调函数，
知
………………8分
（3）
上是增函数，
………………12分
21．（1）证明：①因为
当且仅当
因为
………………3分
②因为
，由①得
（i）
下面证明：对于任意
成立。
根据（i）、（ii）得
………………9分
（2）解：由
从而
因为
………………11分
当
………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com