题目列表(包括答案和解析)
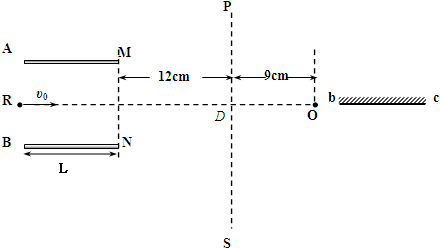
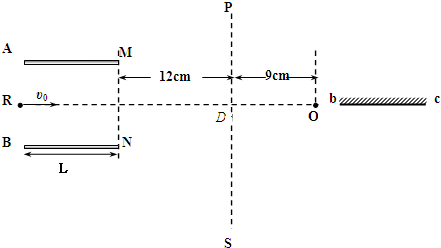
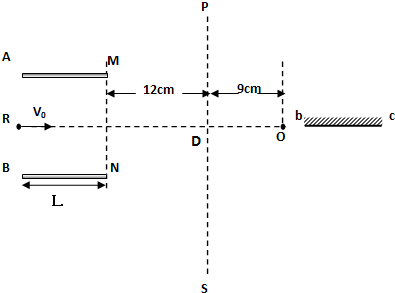
如图所示，两平行金属板A、B长L=8cm，两板间距离d=8cm，A板比B板电势高300V，一个不计重力的带正电的粒子电荷量q=10-10C，质量m=10-20kg，沿电场中心线RD垂直电场线飞入电场，初速度υo=2×106m/s，粒子飞出平行板电场后可进入界面MN、PS间的无电场区域．已知两界面MN、PS相距为12cm，D是中心线RD与界面PS的交点．求：一、选择题（本题包括12小题，共48分）
1
2
3
4
5
6
7
8
9
10
11
12
CD
B
C
AC
C
B
BD
C
B
D
CD
A
二、实验题（本题共两小题，共17分）
13、⑴ 1.10 （2分）（说明：有效数字不正确不给分）
⑵ 0.765 （3分）（说明：有效数字不正确不给分）
14、⑴ ①不放B时用秒表测出弹簧振子完成30次全振动的时间t1
②将B固定在A上，用秒表测出弹簧振子完成30次全振动的时间t2（此两步共5分，明确写出只测一次全振动时间的最多给3分）
⑵ 
（3分）
⑶ 无 （1分） 物体与支持面之间没有摩擦力，弹簧振子的周期不变。（3分）
三、计算题（本题包括5小题，共55分）
15、（8分）(说明：其它方法正确按步骤参照给分)
解：对飞鸟，设其最小的飞行速度为v1，则： 
（1分）
对飞机，设其最小起飞速度为v2， 则： 
（1分）
两式相比得:
（1分）
代入数据得:
（2分）
设飞机在跑道上滑行的距离为s，由公式：v2=2as （1分）
得：
=900m
（2分）
16、（10分）(说明：其它方法正确按步骤参照给分)
解:设0～2.0s内物体的加速度大小为a1，2～4s内物体的加速度大小为a2，
由 
得
a1=5m/s2，
（1分）
a2=1m/s2 （1分）
由牛顿第二定律得：
（1分）
（1分）
解得： F=30N （2分）
由图象得：物体在前4s内的位移为：
=8m
（2分）
故水平外力F在4s内所做的功为：
=－240J
（2分）
17、（12分）(说明：其它方法正确按步骤参照给分)
解：⑴设火星表面的重力加速度为
，地球表面的重力加速度为g
由万有引力定律有：
（1分）
可得 
， 
（2分）
设探测器在12m高处向下的速度为
，则根据能量关系有：
（1分）
代入数据，解得 
（1分）
⑵设探测器落地的速度为
，反弹的速度为
，则有：
（1分）
（1分）
代入数据，解得: 
（1分）
（1分）
设“勇气”号和气囊第一次与火星碰撞时所受到的平均冲力为N，
由动量定理得：
（2分）
代入数据，解得：N=4400N （1分）
18、（12分）(说明：其它方法正确按步骤参照给分)
解：⑴设粒子从电场中飞出时的侧向位移为h, 穿过界面PS时偏离中心线OR的距离为y
则： h=at2/2 （1分）
即：
（1分）
代入数据，解得： h=0.03m=3cm （1分）
带电粒子在离开电场后将做匀速直线运动,由相似三角形知识得：
（1分）
代入数据，解得: y=0.12m=12cm （1分）
⑵设粒子从电场中飞出时沿电场方向的速度为vy，则：vy=at= 
代入数据，解得: vy=1.5×106m/s （1分）
所以粒子从电场中飞出时沿电场方向的速度为：
（1分）
设粒子从电场中飞出时的速度方向与水平方向的夹角为θ，则：
（1分）
因为粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏上，所以该带电粒子在穿过界面PS后将绕点电荷Q作匀速圆周运动，其半径与速度方向垂直。
匀速圆周运动的半径：
（1分）
由：
（2分）
代入数据，解得： Q=1.04×10-8C （1分）
19、（13分）(说明：其它方法正确按步骤参照给分)
解：⑴设第1个球与木盒相遇后瞬间，两者共同运动的速度为v1,根据动量守恒定律：
（1分）
代入数据，解得： v1=3m/s （1分）
⑵设第1个球与木盒的相遇点离传送带左端的距离为s，第1个球经过t0与木盒相遇,
则：
（1分）
设第1个球进入木盒后两者共同运动的加速度为a，根据牛顿第二定律：
得： 
（1分）
设木盒减速运动的时间为t1,加速到与传送带相同的速度的时间为t2，则：
=1s
（1分）
故木盒在2s内的位移为零 （1分）
依题意：
（2分）
代入数据，解得： s=7.5m t0=0.5s （1分）
⑶自木盒与第1个球相遇至与第2个球相遇的这一过程中,传送带的位移为S，木盒的位移为s1,则：
（1分）
（1分）
故木盒相对与传送带的位移： 
则木盒与传送带间的摩擦而产生的热量是： 
（2分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com