2008年的汶川大地震震撼了大家的心灵．在地震后大家发现，学习了防震知识且训练有素的学校的师生在地震中伤亡很小；相反的，没有这方面准备的学校损失惨重．为了让大家了解更多的防震避灾的知识，某校举行了一次“防震知识竞赛”，共有800名学生参加了这次竞赛．为了了解本次竞赛成绩的情况，从中抽取了部分学生的成绩进行统计．但是操作人员不小心将频率分布表局部污损，根据这个污损的表格解答下列问题：
（1）若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…，799，
试写出第二组第一位学生的编号；
（2）填充频率分布表的空格（将答案直接填在表格内），并作出频率分布直方图；
（3）若成绩在85.5～95.5分的学生为二等奖，问参赛学生中获得二等奖的学生约为多少人？

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

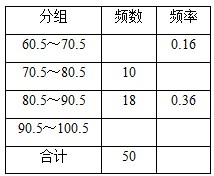2008年的汶川大地震震撼了大家的心灵．在地震后大家发现，学习了防震知识且训练有素的学校的师生在地震中伤亡很小；相反的，没有这方面准备的学校损失惨重．为了让大家了解更多的防震避灾的知识，某校举行了一次“防震知识竞赛”，共有800名学生参加了这次竞赛．为了了解本次竞赛成绩的情况，从中抽取了部分学生的成绩进行统计．但是操作人员不小心将频率分布表局部污损，根据这个污损的表格解答下列问题：
（1）若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…，799，
试写出第二组第一位学生的编号；
（2）填充频率分布表的空格（将答案直接填在表格内），并作出频率分布直方图；
（3）若成绩在85.5～95.5分的学生为二等奖，问参赛学生中获得二等奖的学生约为多少人？

查看答案和解析>>

1―5AACBB    6―8DCB

二、填空题：本大题共6个小题，每小题5分，共30分。

9．                10．                   11．6

12．         13．①和③  或①和④             14．

三、解答题：本大题共6个小题，共80分。

15．解（I）该灯泡的使用寿命不足1500小时的概率 ……6分

   （II）至多有2只灯泡使用寿命不足1500小时的概率……12分

答：从这1000只灯泡中任选1只灯泡使用寿命不足1500小时的概率等于

   从这1000只灯泡中任选3只，至多有2只灯泡使用寿命不足1500小时的概率等于。                                                  ……13分

16．（本小题共13分）

解：（I）由已知得          ……5分

    又在锐角△ABC中，所以A=60°，[不说明是锐角△ABC中，扣1分]……7分

   （II）因为a=2，A=60°所以  ……9分

    而                         ……11分

    又                        ……13分

    所以△ABC面积S的最大值等于

17．（本小题共13分）

解：（I）               ……3分

    由图知        ……5分

   （II）

                          ……6分

令

当

故函数F（x）的单调增区间是，单调减区间  ……8分

当故函数F（x）的单调增区间是……10分

当a=0时，故函数F（x）的单调增区间是……12分

综上所述：

当函数F（x）的单调增区间是，单调减区间是。

当时，函数F（x）的单调增区间是。              ……13分

18．（本小题共14分）

解：（I）在平面A’FA内过点 A’作A’H⊥垂足为H

    因为    ……4分

    所以               ……6分

    即点A′在平面ABC上的射影在线段AF上         ……7分

  （II）由（I）知，又A′E……9分

   则点H为正

   因为……11分

而，所以二面角的大小为……13分

二面角的大小即为当所旋转过的角的大小。

故所求角等于                                          ……14分

19．（本小题共14分）

    解：（I）由已知……2分

     ……5分

所以当有最小值为-7；

     当有最大值为1。                        ……7分

   （II）设点  直线AB方程：

         ……※

有 ……9分

因为为钝角，

所以    ……12分

解得，此时满足方程※有两个不等的实根……14分

故直线l的斜率k的取值范围  

20．（本小题共14分）

解：（I）因为数列是等差数列，公差为2

    （II）又

，与已知矛盾，所以3

当时，  所以=4  ……8分

    （III）由已知当=4时，

令

所以数列{a_n}的前n项和

……14分