题目列表(包括答案和解析)
(本小题满分12分)
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
⑴ 画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
⑵ 计算甲种商品重量误差的样本方差；
⑶ 现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽中的概率
（本小题满分12分）为了了解某年段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.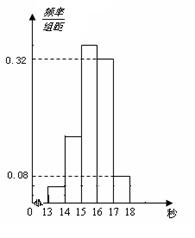
⑴将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
⑵求调查中随机抽取了多少个学生的百米成绩；
⑶若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.
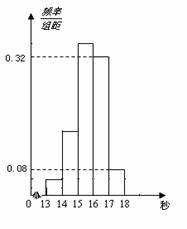
（本小题满分12分）为了了解某年段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.
（Ⅰ）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
（Ⅱ）求调查中随机抽取了多少个学生的百米成绩；
（Ⅲ）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.
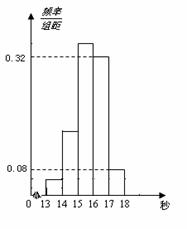
（本小题满分12分）为了了解某年段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.
（Ⅰ）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
（Ⅱ）求调查中随机抽取了多少个学生的百米成绩；
（Ⅲ）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.
一、填空题
1．
2．
3．既不充分条件又不必要条件 4．[－4，－π]
[0，π]
5．
6．6 7．
8．2个 9．等腰直角三角形
10．
11．（-3，4），（-1，2）
12．①、②、⑤
13．
14．C
二、解答题
15．（本小题满分14分）
解：（1）设
由
得
它的解集为（1，3）得方程
的两根为1和3且a<0
即
……（1）
……3分
有等根得
……（2）
……6分
由(1)(2)及
得
故
的解析式为
……8分
（2）由
及
……10分
由
……12分
解得 
……14分
16．（本小题满分14分）
解：由
得
，
………………………………2分
又
， ……………………………………6分
由
得
, …………………………10分
．
……14分
17．（本小题满分15分）．
已知二次函数的二次项系数为
，且不等式的解集为
．
（1）若方程
有两个相等的根，求的解析式；
（2）若的最大值为正数，求的取值范围．
解：（1）设由得
它的解集为（1，3）得方程的两根为1和3且a<0
即 ……（1）
……3分
有等根得
……（2）
……6分
由(1)(2)及得
故的解析式为
……8分
（2）由
及
……10分
由
……12分
解得 ……15分
18解：（1）当m＝2时，A＝（-2，2），B＝（-1，3）∴ A
B＝（-1，2）．……5分
（2）当m＜0时，B＝（1+m，1-m）
要使B
A，必须
，此时
m
当m＝0时，B＝
，BA；适合
……10分
当m＞0时，B＝（1-m，m＋1）
要使BA，必须
，此时0<m≤1． ……13分
∴综上可知，使BA的实数m的取值范围为[-1，1] ……15分
法2
要使BA，必须
，此时m1； ……13分
∴使BA的实数m的取值范围为[-1，1] ……15分
18．（本小题满分15分）
（1）解：由
得
，
． ………………2分
设
=
＜0(讨论a＞1和0＜a＜1)，
得f(x)为R上的增函数． ………………5分
（2）由
， …………7分
即
得
， ………………9分
得1＜m＜
.
………………10分
（3）f(x)在R上为增函数)f(x) 当
时)f(x)-4的值恒为负数， ………13分
而f(x)在R上单调递增得f(2)-40，
………………15分
19．（本小题满分16分）
解：（1）∵f（x+1）为偶函数，
∴
恒成立，
即（
∴
．
∵函数f（x）的图象与直线y=x相切，
∴二次方程
有两相等实数根，
∴
………………6分
（2）
………………8分
即
为方程
的两根
．
………………11分
∵m＜n且
．
故当
；
当k＞1时，
当k=1时，[m，n]不存在． ………………16分
20．（本小题满分16分）
解：（1）若
为函数f(x)不动点，则有
，
整理得 
①
………………2分
根据题意可判断方程①有两个根，且这两个根互为相反数，得
>
，
<0
所以b=3 ,a>0 ………………4分
而
，所以
．
即b=3，a>0，且a≠9. ………………5分
（2）在（1）的条件下，当a=8时，
．
由
，解得两个不动点为
，……6分
设点P(x ,y),则y>3 ,即
>3解得x<-3 ．
………………8分
设点P(x，y)到直线A
．
………………10分
当且仅当
，即x=―4时，取等号，此时P(―4，4)． ……12分
（3）命题正确． ………………13分
因为f(x)定义在R上的奇函数，所以f(―0)=―f(0) ,所以0是奇函数f(x)的一个不动点．
设c≠0是奇函数f(x)的一个不动点,则f(c)=c
,由
，所以―c也是f (x)的一个不动点．
所以奇函数f(x)的非零不动点如果存在,则必成对出现，故奇函数f(x)的不动点数目是奇数个． ………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com