
题目列表(包括答案和解析)
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
|
| 2 |
| cosθ-sinθ |
| 2 |
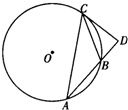 A.(不等式选做题)
A.(不等式选做题)| 3 |
| π |
| 3 |
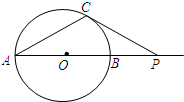 A.不等式
A.不等式| x-2 |
| x2+3x+2 |
| 3 |
|
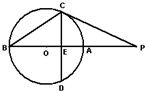 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为| π |
| 4 |
| 2 |
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
A
D
B
A
A
C
C
D
D
12.提示:由于 是中点,
是中点, 中,
中, ,
,
 ,
,
所以 ,所以
,所以
二、填空题
13. 14. 52 15.
14. 52 15.  16. 18
16. 18
16.提示:由 可得
可得 ,则
,则 ,所以
,所以 ,所以
,所以 ,
, ,所以
,所以 ;
; 当且仅当
当且仅当 时成立
时成立
三、解答题
17.解:由
 (3分)
(3分)

 (6分)
(6分)
(2)由(1)知
 (8分)
(8分)
 (10分)
(10分)


 (13分)
(13分)
18.解: , (2分)
, (2分)
由 ,得
,得
 (4分)
(4分)
则 (5分)
(5分)
由于 ,于是有:
,于是有:
(1)当 时,不等式的解集为
时,不等式的解集为 (8分)
(8分)
(2)当 时,不等式的解集为
时,不等式的解集为 (11分)
(11分)
(3)当 时,不等式的解集为
时,不等式的解集为 (13分)
(13分)
19.解:(Ⅰ)由 成等差数列,
成等差数列,
得 , (2分)
, (2分)
即  (5分)
(5分)
(Ⅱ) (7分)
(7分)
∵ (9分)
(9分)
∵ (11分)
(11分)
∴ (12分)
(12分)
20.解:(1)由题 ,
, (2分)
(2分)
 等差数列的公差
等差数列的公差
 (4分)
(4分)
 (5分)
(5分)
(2) ,
,
令 ①
①
 ② (7分)
② (7分)
则②-①可得:
 (9分)
(9分)

而 (11分)
(11分)
 (12分)
(12分)
21.解:(1)由 为奇函数,则
为奇函数,则 ,所以
,所以 ,得:
,得: (3分)
(3分)
(2)由(1)可知 (5分)
(5分)
又 ,
,

所以 (7分)
(7分)
(3)由 得:
得:
则 (8分)
(8分)
令


下求 :令
:令 , 由于
, 由于

则

 (10分)
(10分)
当 时,
时, 与
与 均递增,所以
均递增,所以 递增,
递增,
所以当 时
时 取最大值为
取最大值为 所以
所以 (12分)
(12分)
22.解:(Ⅰ) ∴
∴ (1分)
(1分)
当 时,
时,
 ,即
,即 是等比数列.
(3分)
是等比数列.
(3分)
∴ ; (4分)
; (4分)
(Ⅱ)由(Ⅰ)知, ,若
,若 为等比数列,
为等比数列,
则有 而
而
故 ,解得
,解得 ,
,
再将 代入得
代入得 成立,
成立,
所以 . (8分)
. (8分)
(III)证明:由(Ⅱ)知 ,所以
,所以

 ,
,
由 得
得
所以 ,
,
从而

 .
(12分)
.
(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com