
题目列表(包括答案和解析)
.设 ,…,
,…,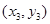 是变量
是变量 和
和 的
的 个样本点,直线
个样本点,直线 是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )
是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )
(A) 和
和 的相关系数为直线
的相关系数为直线 的斜率
的斜率
(B) 和
和 的相关系数在0到1之间
的相关系数在0到1之间
(C)当 为偶数时,分布在
为偶数时,分布在 两侧的样本点的个数一定相同
两侧的样本点的个数一定相同
(D)直线 过点
过点

从0,1,2,3中选取三个不同的数字组成一个三位数,则不同的三位数有( )
| A.24个 | B.20个 | C.18个 | D.15个 |
| 满意 | 不满意 | 总计 | |
| 文科 | 22 | 18 | 40 |
| 理科 | 48 | 12 | 60 |
| 总计 | 70 | 30 | 100 |
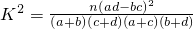 其中n=a+b+c+d)
其中n=a+b+c+d)| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
一、选择题答题卡
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
D
D
A
B
B
C
B
C
二、填空题:
11. ___2____ 12.__29_______ 13.___ ③_____ 14___2____ 15. ____ (2,2) ___ (4,402)
三、解答题:
16.(本小题满分12分)
解:(I)./file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image170.gif) ………(2分)
………(2分)
因此,函数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image172.gif) 图象的对称中心为
图象的对称中心为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image174.gif) ,……………………………………(4分)
,……………………………………(4分)
对称轴为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image176.gif) .…………………………………………………………(6分)
.…………………………………………………………(6分)
(Ⅱ)因为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image178.gif) 在区间
在区间/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image180.gif) 上为增函数,在区间
上为增函数,在区间/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image182.gif) 上为减函数,又
上为减函数,又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image184.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image186.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image188.gif) ……(10分)
……(10分)
故函数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image172.gif) 在区间
在区间/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image128.gif) 上的最大值为
上的最大值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image192.gif) ,最小值为-1.……………….(12分)
,最小值为-1.……………….(12分)
17.解:(I)∵z,y可能的取值为2、3、4,
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image194.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image196.gif)
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image198.gif) ,且当x=2,y=4,或x=4,y=2时,
,且当x=2,y=4,或x=4,y=2时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image200.gif) .…………………… (3分)
.…………………… (3分)
因此,随机变量/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif) 的最大值为3.
的最大值为3.
∵有放回地抽两张卡片的所有情况有3×3=9种,
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image203.gif) .
.
答:随机变量的最大值为3,事件“/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif) 取得最大值”的概率为
取得最大值”的概率为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image206.gif) . ……………(5分)
. ……………(5分)
(II) /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif) 的所有取值为0,1,2,3.
的所有取值为0,1,2,3.
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif) =0时,只有x=3,y=3这一种情况,
=0时,只有x=3,y=3这一种情况,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif) =1时,有x=2,y=2或x=3,y=2或x=3,y=4或x=4,y=4四种情况,
=1时,有x=2,y=2或x=3,y=2或x=3,y=4或x=4,y=4四种情况,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif) =3时,有x=2,y=3或x=4,y=3两种情况.
=3时,有x=2,y=3或x=4,y=3两种情况.
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image208.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image210.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image212.gif) ………………………………(10分)
………………………………(10分)
则随机变量/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif) 的分布列为:
的分布列为:
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image132.gif)
0
1
2
3
P
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image214.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image216.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image206.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image206.gif)
因此,数学期望/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image220.gif) .…………………….(12分)
.…………………….(12分)
18.(本小题满分12分)
解:(I)∵A
∴A
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image140.gif) ,AB=AC=2
,AB=AC=2
∴∠BAC=60°,∴△ABC为正三角形,即AD⊥BC.…………………(3分)
又A
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image223.gif) ,∴平面A1 AD⊥平面BCC1B1.………………… (6分)
,∴平面A1 AD⊥平面BCC1B1.………………… (6分)
则A(0,0,0),B(2,0,0),C(1,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image227.gif) ,0),
,0),
A1(0,0, /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image227.gif) ),B1(1,0,
),B1(1,0,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image227.gif) ),
),
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image230.gif) ,
,
显然,平面ABB
设平面BCC1B1的法向量为n=(m,n,1),则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image232.gif)
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image234.gif) ∴
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image236.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image238.gif) ,…………………………………………………………………(10分)
,…………………………………………………………………(10分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image240.gif)
即二面角A-BB1-C为arccos/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image242.gif) …………………………………………(12分)
…………………………………………(12分)
19.(本小题满分13分) ,
解:(I)依题意,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image244.gif) ,
, /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image246.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image248.gif) ……………………………
(3分)
……………………………
(3分)
(Ⅱ) 依题意,棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第一n-2站,又掷出3或4或5或6,其概率为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image250.gif) ;第二种,棋子先到第n -1站,又掷出1或2,其概率为
;第二种,棋子先到第n -1站,又掷出1或2,其概率为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image252.gif) …………………………………………
(5分)
…………………………………………
(5分)
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image254.gif)
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image256.gif)
即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image258.gif) …………………… (8分)
…………………… (8分)
(Ⅲ)由(Ⅱ)可知数列/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image260.gif) (1≤n≤99)是首项为
(1≤n≤99)是首项为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image262.gif) ,公比为
,公比为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image264.gif) 的等比数列……………………………………………………………………… (10分)
的等比数列……………………………………………………………………… (10分)
于是有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image266.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image268.gif)
因此,玩该游戏获胜的概率为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image270.gif) ………………………………
(13分)
………………………………
(13分)
20.(本小题满分12分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image146.jpg)
解:(I)由题意知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image272.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image274.gif) 是等差数列.…………………………………………2分
是等差数列.…………………………………………2分
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image276.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image278.gif) ………………………………5分
………………………………5分
(II)由题设知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image280.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image282.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image284.gif) 是等差数列.…………………………………………………………8分
是等差数列.…………………………………………………………8分
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image286.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image288.gif) ………………………………10分
………………………………10分
∴当n=1时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image290.gif) ;
;
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image292.gif)
经验证n=1时也适合上式. /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image294.gif) …………………………12分
…………………………12分
21.(本题14分)
解:(Ⅰ) 由条件得
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image296.gif) ,设直线AB的方程为
,设直线AB的方程为
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image298.gif)
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image300.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image302.gif)
∴由韦达定理得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image304.gif)
从而有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image306.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image308.gif)
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image310.gif)
(Ⅱ)抛物线方程可化为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image312.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image314.gif)
∴切线NA的方程为:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image316.gif)
切线NB的方程为:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image318.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image320.gif)
从而可知N点、Q点的横坐标相同但纵坐标不同。
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image322.gif) ∥
∥/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image164.gif)
又由(Ⅰ)知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image325.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image327.gif)
而/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image329.gif)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image331.gif)
(Ⅲ)由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image333.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image335.gif) 由于
由于
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image337.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image339.gif)
从而/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image341.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image343.gif) 又
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image345.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image347.gif) 而
而/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image349.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image351.gif)
而p>0,∴1≤p≤2
又p是不为1的正整数
∴p=2
故抛物线的方程:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image353.gif)
w.w.w.k.s.5.u.c.o.m
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(2).files\image343.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com