
题目列表(包括答案和解析)
(1)只有一只水龙头供水时,应如何安排这十个人打水的次序,使他们的总的花费时间最少?这个最少时间是多少?
(2)若有两个相同的水龙头供水时,应如何安排这十个人的次序,使他们的总的花费时间最少?这个最少时间是多少?
| 4 |
| 5 |
| 24 |
| 125 |
| 6 |
| 125 |
 ,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为
,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为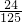 ,该同学3门课程都未获得优秀的概率为
,该同学3门课程都未获得优秀的概率为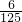 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立. ,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为
,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为 ,该同学3门课程都未获得优秀的概率为
,该同学3门课程都未获得优秀的概率为 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com