如图所示.真空中有(.0)为圆心.半径为的圆柱形匀强磁场区域.磁场的磁感应强度大小为B.方向垂直于纸面向里.在的虚线上方足够大的范围内.有方向水平向左的匀强电场.电场强度的大小为,从点向不同方向发射速——青夏教育精英家教网—

如图所示.真空中有(.0)为圆心.半径为的圆柱形匀强磁场区域.磁场的磁感应强度大小为B.方向垂直于纸面向里.在的虚线上方足够大的范围内.有方向水平向左的匀强电场.电场强度的大小为,从点向不同方向发射速率相同的质子.质子的运动轨迹均在纸面内.设质子在磁场中的偏转半径也为.已知质子的电量为.质量为.不计重力及阻力的作用.求 (1)质子射入磁场时的速度大小【查看更多】

题目列表(包括答案和解析)

如图所示，真空中有(r，0)为圆心，半径为r的圆柱形匀强磁场区域，磁场的磁感应强度大小为B，方向垂直于纸面向里，在y=r的虚线上方足够大的范围内，有方向水平向左的匀强电场，电场强度的大小为E，从O点向不同方向发射速率相同的质子，质子的运动轨迹均在纸面内，设质子在磁场中的偏转半径也为r，已知质子的电量为e，质量为m，不计重力及阻力的作用，求：
(1)质子射入磁场时的速度大小；
(2)速度方向沿x轴正方向射入磁场的质子，到达y轴所需的时间；
(3)速度方向与x轴正方向成30°角（如图中所示）射入磁场的质子，到达y轴的位置坐标。

查看答案和解析>>

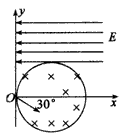
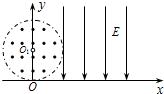如图所示，真空中有以O₁为圆心，半径为r=10cm的圆形匀强磁场区域，坐标原点O为圆形磁场边界上的一点．磁场的磁感应强度大小为B=0.2T，方向垂直于纸面向外．在x≥r的空间内分布有方向竖直向下、大小为E=4×10⁵V/m的匀强电场．现有一质子源从O点向纸面内的各个不同方向发射质子，速率均为v=2.0×10⁶m/s，设质子质量为m=1.6×10^-27kg（不计质子的重力），电荷q=1.6×10^-19C．求
（1）沿y轴正方向射入磁场的质子到达x轴所需的时间；
（2）沿与x轴正方向成60°角射入磁场的质子到达x轴时的位置．

查看答案和解析>>

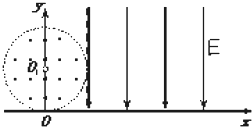如图所示，真空中有以O₁为圆心，r为半径的圆形匀强磁场区域，坐标原点O为圆形磁场边界上的一点．磁场的磁感应强度大小为B，方向垂直于纸面向外．x=r的虚线右侧足够大的范围内有方向竖直向下、大小为E的匀强电场．从O点在纸面内向各个不同方向发射速率相同的质子，设质子在磁场中的偏转半径也为r，已知质子的电荷量为e，质量为m．求：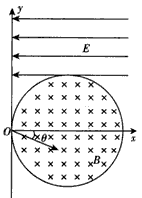
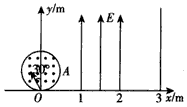
（1）质子射入磁场时的速度大小；
（2）速度方向沿y轴正方向射入磁场的质子到达x轴所需的时间；
（3）速度方向与y轴正方向成37°角且与x轴正方向成127°角射入磁场的质子到达x轴时的位置坐标．（已知sin37°=0.6，cos37°=0.8）

查看答案和解析>>

如图所示，真空中有一以(r，0)为圆心、半径为r的圆柱形匀强磁场区域，磁场的磁感应强度大小为B方向垂直纸面向里，在y≥r的范围内，有方向向左的匀强电场，电场强度大小E。从O点向不同方向发射速率相同的质子，质子的运动轨迹均在纸面内，已知质子的电量为e，质量为m，质子在磁场中的偏转半径也为r，不计重力及阻力作用。求：
(1)质子进入磁场时的速度大小；
(2)速度方向沿x轴正方向射入磁场的质子，到达y轴所需的时间；
(3)速度方向与x轴正方向成30°角（如图中所示）射入磁场的质子，到达y轴时的位置坐标。

查看答案和解析>>

如图所示，真空中有一个半径r=0.5 m的圆柱形匀强磁场区域，x轴为磁场边在O点的切线，O点为坐标系的原点，磁场的磁感应强度大小B=2×10^-3 T，方向垂直于纸面向外，在x=1 m和x=2 m之间的区域内有一个方向沿y轴正方向的匀强电场区域，电场强度E=1.5×10³ N/C。在x=3 m处有一与x轴垂直的足够长的荧光屏，有一个粒子源从O点在纸平面内向各个方向发射速率相同、比荷的带正电的粒子，不计粒子的重力及粒子间的相互作用和其他阻力，求：
(1)沿y轴正方向射入磁场又恰能从磁场最右侧的A点离开磁场的粒子进入电场时的速度和在磁场中运动的时间；
(2)与y轴正方向成30°角（如图所示）射人磁场的粒子从进入电场到打到荧光屏上的时间；
(3)从O点处向不同方向发射的带电粒子打在荧光屏上的区域范围（用位置坐标表示）。

查看答案和解析>>

一、选择题：1、C 2、BD 3、A 4、B 5、AB 6、BCD 7、C 8、A

9、C 10、AD 11、BC 12、C

二、实验题（本题共2小题共18分）将答案填在横线上或作图和连线.

学科网(Zxxk.Com) 13、（6分）CFEBAD

14、（12分）（1）E；C

（2）甲

（3）连接实物图

（4）①变大 ②10Ω

（1）每空1分（2）2分（3）4分（4）每空2分。

三、本大题共四小题共计54分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位

15、（12分）（1）两物体第一次并排时蟑螂下降了H/2，两物体速度大小总是相等，可以从能量角度分析。

（2分）

由此得（2分）

（2）蟑螂在垂直于下降物体侧面跳开时具有竖直速度，这等于它所离开的物体的速度，这样跳运并不影响此物体速度。但是当蟑螂抓住第二个物体侧面后，系统速度变了。系统的一部分能量转变为内能。可等效处理，根据动量守恒定律求新速度。两物体以速度v₁一起运动，蟑螂以同样大小、但相反方向的速度迎面飞去，经这样“碰撞”后速度为

（1分）