
题目列表(包括答案和解析)
(本小题满分8分)已知函数![]()
![]() ,其中
,其中![]() ,
,
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式
的解析式
(2)讨论函数![]() 的单调性
的单调性
(本小题满分8分)在数列![]() 中,
中,![]()
(1)求![]() ;
;
(![]() 2)求数列
2)求数列![]() 的前n项和
的前n项和![]() .
.
(本小题满分8分)
已知全集U=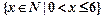 ,集合A={
,集合A={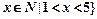 ,集合B=
,集合B=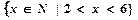
求:(1)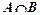
 (2)
(2) 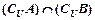
(本小题满分8分)
设全集U="{1," 2, 3, 4, 5}, 集合A="{1," a2-1, 4}, 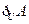 ="{2," a+3}
="{2," a+3}
(I)求a值;
(II)满足AÍBU这样的集合B共有几个?试将这样的B集合都写出来
(本小题满分8分)
某交易市场的土豆在30天内每吨的交易价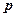 (千元)与时间
(千元)与时间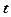 (天)(
(天)(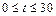 ),组成有序数对
),组成有序数对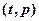 ,点
,点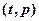 落在如图所示的两条线段上,该市场土豆在30天内的日交易量
落在如图所示的两条线段上,该市场土豆在30天内的日交易量 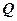 (吨)与时间
(吨)与时间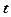 (天)的部分数据如下表所示
(天)的部分数据如下表所示
第 天 天 | 4 | 10 | 16 | 22 |
 (吨) (吨) | 36 | 30 | 24 | 18 |
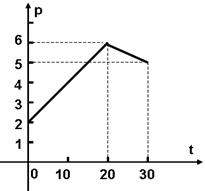
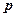 (千元)与时间
(千元)与时间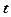 (天)所满足函数关系式;
(天)所满足函数关系式;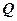 (吨)与时间
(吨)与时间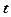 (天)的一次函数解析式;
(天)的一次函数解析式; 表示日交易额(千元),写出
表示日交易额(千元),写出 关于
关于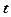 的函数解析式,问这30天中第几天交易额最大,最大值多少?
的函数解析式,问这30天中第几天交易额最大,最大值多少?一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
B
B
D
B
D
C
A
B
C
A
D
二、填空题
13、(-¥,-1)È(2,+¥) 14 、2n ?
1 15、45 16、 17、0.94 18、
17、0.94 18、
三、解答题
19、解: 设等比数列{an}的公比为q, 则q≠0, a2= = , a4=a3q=2q
所以 + 2q= , 解得q1= , q2= 3,
当q1=, a1=18.所以 an=18×()n-1= = 2×33-n.
当q=3时, a1= , 所以an=×3n-1=2×3n-3
 20、解:(1)将函数解析式变形为
20、解:(1)将函数解析式变形为


 (2)方程f(x)=5的解分别是
和 , 由于f(x)在(-∞,-1]和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此
(2)方程f(x)=5的解分别是
和 , 由于f(x)在(-∞,-1]和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此
 .
.
 由于
由于
21、解:(1)当a=2时,A=(2,7),B=(4,5)∴ A B=(4,5)
B=(4,5)
(2)∵ B=(
当a< 时,A=(
时,A=( A,必须
A,必须 ,此时a=-1;
,此时a=-1;
当a= 时,A=
时,A= ,使B
,使B A的a不存在;
A的a不存在;
当a> 时,A=(2,
时,A=(2, A,必须
A,必须 ,此时1≤a≤3.
,此时1≤a≤3.
综上可知,使B A的实数a的取值范围为[1,3]∪{-1}
A的实数a的取值范围为[1,3]∪{-1}
22、解:(Ⅰ)求导得 。
。
由于  的图像与直线
的图像与直线 相切于点
相切于点 ,
,
所以 ,即:
,即:
 1
1 .
.
3
(Ⅱ)由 得:
得:
令f′(x)>0,解得 x<-1或x>3;又令f′(x)< 0,解得 -1<x<3.
故当x (
( , -1)时,f(x)是增函数,当 x
, -1)时,f(x)是增函数,当 x (3,
(3, )时,f(x)也是增函数,
)时,f(x)也是增函数,
但当x (-1 ,3)时,f(x)是减函数.
(-1 ,3)时,f(x)是减函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com