
题目列表(包括答案和解析)
数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 。
。
![]() (1)求数列
(1)求数列![]() 的通项公式;
的通项公式;
![]() (2)设等差数列
(2)设等差数列![]() 各项均为正数,满足
各项均为正数,满足![]() ,且
,且![]() ,成等比数列。证明:
,成等比数列。证明:![]() 。
。
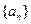 的前
的前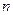 项和为
项和为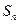 ,且
,且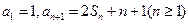 。
。 (1)求数列
(1)求数列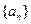 的通项公式;
的通项公式; (2)设等差数列
(2)设等差数列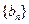 各项均为正数,满足
各项均为正数,满足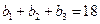 ,且
,且 ,成等比数列。证明:
,成等比数列。证明: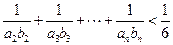 。
。
数列![]() (n∈N*)是递增的等比数列,且
(n∈N*)是递增的等比数列,且![]() 数列{
数列{![]() }满足
}满足![]()
(I)求数列![]() 的通项公式:
的通项公式:
(II)设数列![]() 是否存在正整数n,使得数列
是否存在正整数n,使得数列![]() 前n项和为
前n项和为![]() ?若存在,求出n的值;若不存在,请说明理由。
?若存在,求出n的值;若不存在,请说明理由。
定义:若数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“平方递推数列”。已知数列
为“平方递推数列”。已知数列![]() 中,
中,![]() ,点
,点![]() 在函数
在函数![]() 的图像上,其中
的图像上,其中![]() 为正整数。
为正整数。
(1)证明:数列![]() 是“平方递推数列”,且数列
是“平方递推数列”,且数列![]() 为等比数列。
为等比数列。
(2)设(1)中“平方递推数列”的前![]() 项之积为
项之积为![]() ,即
,即![]()
![]() ,求数列
,求数列![]() 的通项及
的通项及![]() 关于
关于![]() 的表达式。
的表达式。
(3)记![]() ,求数列
,求数列![]() 的前
的前![]() 项之和
项之和![]() ,并求使
,并求使![]()
![]() 的
的![]() 的最小值。
的最小值。
一、选择题:本题考查基础知识和基本运算. 每题5分,满分50分
1.B 2.D 3.A 4.B 5.C 6.A 7.C 8.B 9.B 10.D
二、填空题:本题考查基础知识和基本运算. 每题4分,满分20分.
11. 5 12.卷.files/image207.gif)
三、解答题:本题共6大题,共80分.解答应写出文字说明、证明过程或演算步骤.
16. 本题主要考查三角函数性质、三角恒等变换等基本知识,考查推理和运算能力.满分13分。
解:(Ⅰ)
卷.files/image209.gif)
(2)
卷.files/image211.gif)
17. 本题主要考查线面平行与垂直关系,及多面体的体积计算等基础知识,考查空间想象能力,逻辑思维能力和运算能力.同时也可考查学生灵活利用图形,建立空间直角坐标系,借助向量工具解决问题的能力。满分13分。
解:(1)证明:卷.files/image213.gif) EF 分别是DD1 DA1的中点, EF A1D1
EF 分别是DD1 DA1的中点, EF A1D1
又 A1D1 B
EF 平面A1BC
(2) 法一: AB AD AA1两两垂直,以AB所在直线为
轴,以 AD所在直线轴,以AA1所在直线为 轴,建立空间直角坐标系如图,设BC=1
则 卷.files/image215.gif) 设平面A1CD的法向量
设平面A1CD的法向量
卷.files/image217.gif)
卷.files/image219.gif)
卷.files/image221.gif)
卷.files/image223.gif)
卷.files/image225.gif)
18.本题主要考查频率分布直方图、随机变量的分布列及数学期望等概率与统计的基础知识,考查运算求解能力、数据处理能力、分析与解决问题能力及必然与或然的数学思想、应用意识等。满分13分。
解:(1)设任意抽取一家企业,抽到不合格企业、合格企业、良好企业、优秀企业的概率分别是p1、p2、p3、p4
则根据频率分布直方图可知:
卷.files/image227.gif)
卷.files/image229.gif)
(2) 设整改后,任意抽取一家企业,抽到不合格企业、合格企业、良好企业的概率分别为
卷.files/image231.gif) ,
,
卷.files/image233.gif)
卷.files/image235.jpg)
卷.files/image237.gif)
19.本题主要考查向量、直线、抛物线等基础知识及轨迹的求解方法,考查函数与方程思想、分类与整合思想及运算求解能力、探究能力、分析问题和解决问题的能力。满分13分
解:(1)
卷.files/image239.gif)
(2)
卷.files/image241.gif)
20. 本题主要考查二次函数及其性质、导数的基本知识,几何意义及其应用,同时考查考生分类讨论思想方法及化规的能力:
解:(1)依题意设卷.files/image243.gif) ,由
,由卷.files/image245.gif) (
(卷.files/image247.gif) 为
为卷.files/image249.gif) 边上的高)。
边上的高)。
卷.files/image251.gif) 或3,
或3,卷.files/image253.gif)
卷.files/image255.gif) 或
或卷.files/image257.gif) (或讨论
(或讨论卷.files/image166.gif) 与
与卷.files/image260.gif) )。
)。
或依题意卷.files/image262.gif) 或3,其它同上
或3,其它同上
(2)当时卷.files/image166.gif) ,
,卷.files/image265.gif)
卷.files/image267.gif) 令
令卷.files/image269.gif) 得
得卷.files/image271.gif) ,或
,或卷.files/image273.gif)
卷.files/image275.jpg)
卷.files/image277.gif) 不是极值点,
不是极值点,卷.files/image273.gif) 是极值点,
是极值点,
因此,函数卷.files/image279.gif) 的极小值为
的极小值为卷.files/image281.gif) ,极大值不存在。
,极大值不存在。
(3)对于卷.files/image257.gif) ,由
,由卷.files/image172.gif) 及
及卷.files/image174.gif) ,得
,得卷.files/image286.gif) ,不合题意,舍去,
,不合题意,舍去,
只能卷.files/image288.gif)
卷.files/image290.gif) 对
对卷.files/image292.gif) 恒成立,
恒成立,
卷.files/image294.gif)
又卷.files/image296.gif) ,
,卷.files/image298.gif)
卷.files/image213.gif) 数列
数列卷.files/image301.gif) 是首项为3,公比为2的等比数列,
是首项为3,公比为2的等比数列,
卷.files/image303.gif) ,
,
卷.files/image305.gif)
为所求。
或卷.files/image307.gif)
21.(1)本题主要考查矩阵与变换、曲线在矩阵变换下的曲线的方程,考查运算求解能力及化归与转化思想。
解:由已知得卷.files/image309.gif) ,矩阵
,矩阵卷.files/image311.gif)
它所对应的变换为卷.files/image313.gif)
解得卷.files/image315.gif) ,把它代入方程为
,把它代入方程为卷.files/image186.gif) 得
得卷.files/image318.gif)
即经过矩阵卷.files/image188.gif) 的变换后的曲线方程
的变换后的曲线方程卷.files/image321.gif) 。
。
(也可先计算卷.files/image323.gif) 再求曲线方程,可相应给分)
再求曲线方程,可相应给分)
(2)本题主要考查直线和椭圆的极坐标与参数方程,考查运算求解能力及化归与转化思想。
解:由卷.files/image193.gif) 可化为直角坐标方程
可化为直角坐标方程卷.files/image325.gif)
参数方程为卷.files/image196.gif) (
(卷.files/image198.gif) 为对数)可化为直角坐标方程
为对数)可化为直角坐标方程卷.files/image327.gif)
联立(1)(2)得两曲线的交点为卷.files/image329.gif)
所求的弦长卷.files/image331.gif)
(3)本题主要考查利用柯西不等式证明不等式,考查推理论证能力。
证明:左边卷.files/image333.gif)
卷.files/image335.gif)
卷.files/image337.gif)
卷.files/image339.gif)
卷.files/image341.gif)
卷.files/image343.gif) 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com