
题目列表(包括答案和解析)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
 (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 交于点C,点M在线段AC上,满足=.
交于点C,点M在线段AC上,满足=.
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 的直线与轨迹M交于
点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为
锐角三角形时t的取值范围.
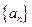 的前
的前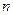 项和为
项和为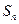 ,对任意的正整数
,对任意的正整数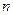 ,都有
,都有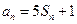 成立,记
成立,记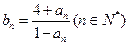 。
。 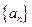 与数列
与数列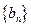 的通项公式;
的通项公式;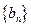 的前
的前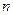 项和为
项和为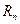 ,是否存在正整数
,是否存在正整数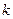 ,使得
,使得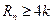 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数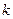 ;若不存在,请说明理由;
;若不存在,请说明理由;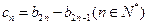 ,设数列
,设数列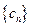 的前
的前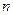 项和为
项和为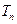 ,求证:对任意正整数
,求证:对任意正整数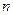 都有
都有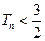 ;
;| 1 |
| an |
| 1 |
| 10 |
(本小题满分12分)
(理科)已知数列 {2 n•an} 的前 n 项和 Sn = 9-6n.
(I) 求数列 {an} 的通项公式;
(II) 设 bn = n·(2-log 2 ),求数列 { } 的前 n 项和Tn.
(文科)已知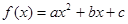 ,且f(0)=8及f(x+1)-f(x)=-2x+1。
,且f(0)=8及f(x+1)-f(x)=-2x+1。
(1)求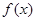 的解析式;
的解析式;
(2)求函数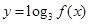 的单调递减区间及值域.
的单调递减区间及值域.
(2009四川卷文)(本小题满分14分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的正整数
,对任意的正整数![]() ,都有
,都有![]() 成立,记
成立,记![]() 。
。
(I)求数列![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(II)设数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(III)记![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对任意正整数
,求证:对任意正整数![]() 都有
都有![]() ;
;
一、选择题:(1)-(12)CAADB BAACD CA
二、填空题:(13) (14)
(14) (15)
(15) (16)
(16)
三、解答题:
(17)解:(1)


 …………6分
…………6分
(2) …………8分
…………8分

 时,
时,
当 时,
时,
当 时,
时, ……11分
……11分
综上所述: ………………12分
………………12分
(18)解:(1)每家煤矿必须整改的概率1-0.5,且每家煤矿是否整改是相互独立的,所以恰好有两家煤矿必须整改的概率是
 ………………4分
………………4分
(2)由题设,必须整改的煤矿数 服从二项分布
服从二项分布 ,从而
,从而 的数学期望是
的数学期望是
 ,即平均有2.50家煤矿必须整改. ………………8分
,即平均有2.50家煤矿必须整改. ………………8分
(3)某煤矿被关闭,即煤矿第一次安检不合格,整改后复查仍不合格,所以该煤矿被关闭的概率是 ,从而该煤矿不被关闭的概率是0.9,由题意,每家煤矿是否关闭是相互独立的,所以5家煤矿都不被关闭的概率是
,从而该煤矿不被关闭的概率是0.9,由题意,每家煤矿是否关闭是相互独立的,所以5家煤矿都不被关闭的概率是

从而至少关闭一家煤矿的概率是 ………………12分
………………12分
(19)证明:由多面体 的三视图知,四棱锥
的三视图知,四棱锥 的底面
的底面 是边长为
是边长为 的正方形,侧面
的正方形,侧面 是等腰三角形,
是等腰三角形, ,
,
且平面 平面
平面 .……2分
.……2分
(1)
 连结
连结 ,则
,则 是
是 的中点,
的中点,
在△ 中,
中, ,………4分
,………4分
且
 平面
平面 ,
,
 平面
平面 ,
,
∴ ∥平面
∥平面 ………6分
………6分
(2)
因为平面 ⊥平面
⊥平面 ,
,
平面 ∩平面
∩平面 ,
,
又 ⊥
⊥ ,所以,
,所以, ⊥平面
⊥平面 ,
,
∴ ⊥
⊥ …………8分
…………8分
又 ,
, ,所以△
,所以△ 是
是
等腰直角三角形,
且 ,即
,即 ………………10分
………………10分
又 , ∴
, ∴  平面
平面 ,
,
又
 平面
平面 ,
,
所以 平面 ⊥平面
⊥平面 ………………12分
………………12分
(20)解:设
由


即
 ,
,
 ………………6分
………………6分
(2)由题意得 上恒成立。
上恒成立。
即 在[-1,1]上恒成立。
在[-1,1]上恒成立。
设 其图象的对称轴为直线
其图象的对称轴为直线 ,所以
,所以 上递减,
上递减,
故只需, ,即
,即 ………………12分
………………12分
(21)解:(I)由




所以,数列 …………6分
…………6分
(II)由 得:
得:


 …………(1)
…………(1)
 …………(2) …………10分
…………(2) …………10分
(2)-(1)得:

 …………12分
…………12分
(22)解:(Ⅰ)∵
∵直线 相切,
相切,
∴ ∴
∴ …………3分
…………3分
∵椭圆C1的方程是  ………………6分
………………6分
(Ⅱ)∵MP=MF2,
∴动点M到定直线 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线 ………………6分
∴点M的轨迹C2的方程为  …………9分
…………9分
(Ⅲ)Q(0,0),设
∴
∵
∴
∵ ,化简得
,化简得
∴ ………………11分
………………11分
∴
当且仅当  时等号成立 …………13分
时等号成立 …………13分
∵
∴当 的取值范围是
的取值范围是
……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com