如图所示，质量均为m的物体A、B分别与轻质弹簧的两端相连接，静止在水平地面上。质量也为m的小物体C从距A物体h高处由静止开始下落，C与A相碰后立即粘在一起向下运动，以后不再分开，当A和C运动到最高点时，物体B对地面刚好无压力。不计空气阻力，弹簧始终处于弹性限度内，重力加速度为g。求

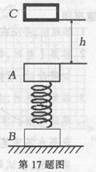
1.A和C一起开始向下运动时的速度大小；

2.A和C运动到最高点时的加速度大小；

3.弹簧的劲度系数k。

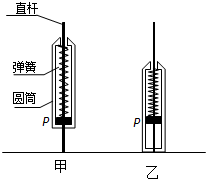
在探究某种笔的弹跳问题时，建立以下简化模型进行研究。

把笔分为轻质弹簧、圆筒和直杆三部分，薄挡板P固定在直杆上，轻质弹簧的两端分别固定在圆筒顶部和薄挡板P上，质量为M的圆筒可沿直杆无摩擦滑动，直杆和挡板P的总质量为m。开始时将笔直立于水平桌面，在桌面上方的矩形区域内有竖直向上的匀强电场，带正电的挡板P非常靠近电场的上边界，挡板P与周围物体绝缘接触，受到的电场力与笔的重力大小相等。向上移动圆筒使弹簧处于原长状态，此时挡板P刚好与圆筒底部接触，如图甲所示。现用力缓慢向下压圆筒，使圆筒底部恰好与水平桌面接触，此过程中压力做功为W，如图乙所示。撤除压力，圆筒弹起并与挡板P碰撞，两者一起上升到最大高度后自由落下，此后直杆在桌面上多次跳动。

       假设圆筒与挡板P每次碰撞结束时均具有相同速度，碰撞时间均忽略不计。直杆与桌面每次碰撞后均不反弹，直杆始终保持竖直状态。不计一切摩擦与空气阻力，重力加速度大小为g，求：

   （1）直杆第一次上升的最大高度h₁；

   （2）直杆运动的总路程h。