练习册

  • 练习册
  • 试题
    (1)通过具体实例.直观了解对数函数模型所刻画的数量关系.初步理解对数函数的概念.体会对数函数是一类重要的函数模型, (2)能借助计算器或计算机画出具体对数函数的图象.探索并了解对数函数的单调性与特殊点, (3)通过比较.对照的方法.引导学生结合图象类比指数函数.探索研究对数函数的性质.培养学生数形结合的思想方法.学会研究函数性质的方法． 【查看更多】

     

    题目列表(包括答案和解析)

    解题过程中究竟选用哪种函数模型，要根据题目具体要求进行抽象和概括，灵活地选取和建立数学模型，常用的数学模型有：

    (1)一次函数模型，其形式为________；

    (2)二次函数模型，其形式为________；

    (3)指数函数模型，其形式为________；

    (4)对数函数模型，其形式为________；

    (5)幂函数模型，其形式为________．

    查看答案和解析>>

    下列说法正确的是（　　）
    A、幂函数的图象恒过（0，0）点B、指数函数的图象恒过（1，0）点C、对数函数的图象恒在y轴右侧D、幂函数的图象恒在x轴上方

    查看答案和解析>>

    下表显示出函数值y随自变量x变化的一组数据，由此可判断它最可能的函数模型为（　　）
    x -2 -1 0 1 2 3
    y
    1
    16
    1
    4
    		 1 4 16 64

    查看答案和解析>>

    下表显示出函数值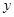随自变量变化的一组数据，由此可判断它最可能的函数模型为

    0

    1

    2

    3

    1

    4

    16

    64

    (    )

    A．一次函数模型      B．二次函数模型     C．指数函数模型      D．对数函数模型

     

    查看答案和解析>>

    11、如表是函数值y随自变量x变化的一组数据，由此判断它最可能的函数模型（　　）

    查看答案和解析>>


    同步练习册答案