题目列表(包括答案和解析)
物理学家James．D．Forbes试图通过水的沸点来估计海拔高度，他知道通过气压计测得的大气压可用于得到海拔高度，气压越低，高度越高，他测量了17个地方水的沸点（℉）及大气压数据，并且对数据作了简单的处理，得到了较为明确的数学关系，所提数据如下：
|
测点编号 |
沸点（℉） |
气压 |
1g（气压） |
100´1g（气压） |
|
1 |
194.5 |
20.79 |
1.3179 |
131.79 |
|
2 |
194.3 |
20.79 |
1.3179 |
131.79 |
|
3 |
197.9 |
22.40 |
1.3502 |
135.02 |
|
4 |
198.4 |
22.67 |
1.3555 |
135.55 |
|
5 |
199.4 |
23.15 |
1.3646 |
136.46 |
|
6 |
199.9 |
23.35 |
1.3683 |
136.83 |
|
7 |
200.9 |
23.89 |
1.3782 |
137.82 |
|
8 |
201.1 |
23.99 |
1.3800 |
138.00 |
|
9 |
201.4 |
24.02 |
1.3805 |
138.05 |
|
10 |
201.3 |
24.01 |
1.3806 |
138.06 |
|
11 |
203.6 |
25.14 |
1.4004 |
140.04 |
|
12 |
204.6 |
26.57 |
1.4244 |
142.44 |
|
13 |
209.5 |
28.49 |
1.4547 |
145.47 |
|
15 |
208.6 |
27.76 |
1.4434 |
144.34 |
|
15 |
210.7 |
29.04 |
1.4630 |
146.30 |
|
16 |
211.9 |
29.88 |
1.4754 |
147.54 |
|
17 |
212.2 |
30.06 |
1.4780 |
147.80 |
（1）试作出气压y=100´1g（气压）关于沸点（℉）的散点图；
（2）根据散点图判断变量x与y的相关关系；计算变量x与y的相关系数；
（3）建立变量x与y的一元线性回归方程。
|
测点编号 |
沸点（℉） |
气压 |
1g（气压） |
100´1g（气压） |
|
1 |
194.5 |
20.79 |
1.3179 |
131.79 |
|
2 |
194.3 |
20.79 |
1.3179 |
131.79 |
|
3 |
197.9 |
22.40 |
1.3502 |
135.02 |
|
4 |
198.4 |
22.67 |
1.3555 |
135.55 |
|
5 |
199.4 |
23.15 |
1.3646 |
136.46 |
|
6 |
199.9 |
23.35 |
1.3683 |
136.83 |
|
7 |
200.9 |
23.89 |
1.3782 |
137.82 |
|
8 |
201.1 |
23.99 |
1.3800 |
138.00 |
|
9 |
201.4 |
24.02 |
1.3805 |
138.05 |
|
10 |
201.3 |
24.01 |
1.3806 |
138.06 |
|
11 |
203.6 |
25.14 |
1.4004 |
140.04 |
|
12 |
204.6 |
26.57 |
1.4244 |
142.44 |
|
13 |
209.5 |
28.49 |
1.4547 |
145.47 |
|
15 |
208.6 |
27.76 |
1.4434 |
144.34 |
|
15 |
210.7 |
29.04 |
1.4630 |
146.30 |
|
16 |
211.9 |
29.88 |
1.4754 |
147.54 |
|
17 |
212.2 |
30.06 |
1.4780 |
147.80 |
（1）试作出气压y=100´1g（气压）关于沸点（℉）的散点图；
（2）根据散点图判断变量x与y的相关关系；计算变量x与y的相关系数；
（3）建立变量x与y的一元线性回归方程。
（本小题满分13分）
为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件，测量产品中的微量元素x,y的含量（单位：毫克）．下表是乙厂的5件产品的测量数据：
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
（1）已知甲厂生产的产品共有98件，求乙厂生产的产品数量；
（2）当产品中的微量元素x,y满足x≥175，且y≥75时,该产品为优等品。用上述样本数据估计乙厂生产的优等品的数量；
（3）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数
的分布列极其均值（即数学期望）。
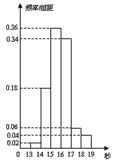
某班50名学生在一次百米测试中，成绩全部介于13秒
与19秒之间，将测试结果按如下方式分成六组：第一
组，成绩大于等于13秒且小于14秒；第二组，成绩大
于等于14秒且小于15秒；……第六组，成绩大于等于
18秒且小于等于19秒。右图是按上述分组方法得到的
频率分布直方图。设成绩小于17秒的学生人数占全班
总人数的百分比为
，成绩大于等于15秒且小于17秒
的学生人数为
，则从频率分布直方图中可分析出和
分别为( )
A．0.9，35 B．0.9，45
C．0.1，35 D．0.1，45
一、选择题
题号
1
2
3
4
5
6
7
8
答案
D
A
B
C
B
B
B
D
二、填空题
9．1； 10．
； 11．12； 12．
； 13．
； 14．
三、解答题
15．解：（Ⅰ）由
，根据正弦定理得
，
所以
，…………………………………………………………………………………………4分
由
为锐角三角形得
．
…………………………………………7分
（Ⅱ）根据余弦定理，得
．
………10分
所以，
．
……………………………………………………………12分
16．解：（1）由题意可知
当
时，
． ……3分
当
时，
，亦满足上式． ……5分
∴数列
的通项公式为
（
）． ……6分
（2）由（1）可知
，
……7分
∴数列
是以首项为
，公比为
的等比数列， ……9分
∴
．
……12分
17．
|
得
…………………2分
，
得
，
……4分
，
的单调区间如下表：
）
，
时，
为极大值，而
，则
恒成立，只需
；
或
。
……………………14分
，其方程为
，代入椭圆方程并化简得：
…………………………2分
，
，
，解得
。
…………………………………………6分
，
………………………10分
……………14分
，∴|AM|＝
…………………………………………………………4分
，即（3x－8）（x－8）> 0
即AN长的取值范围是
……………………………8分
……………………………………… 10分
，y′< 0，∴函数y＝
上为单调递减函数，
（平方米）
米 ……………………………………………………… 14分