
题目列表(包括答案和解析)
设函数f(x)= +bx+1(a、b为实数),F(x)=
+bx+1(a、b为实数),F(x)=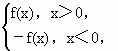
(Ⅰ)若f(-1)=0,且对任意实数均有f(x)≥0成立,求F(x)的表达式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(Ⅲ)若f(x)是偶函数,试判断F(x)的奇偶性.
(Ⅳ)设mn<0,m+n>0,且f(x)是偶函数,求证:F(m)+F(n)>0.
| kx+2 | ||
2
|
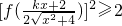 ,其中k∈(-1,1).
,其中k∈(-1,1).| kx+2 | ||
2
|
已知函数f(x)的定义为R,对任意的实数x1、x2都满足f(x1+x2)=f(x1)+f(x2),当x>0时,f(x)>0,且f(2)=3.
(1)试判断f(x)的奇偶性和单调性;
(2)当θ∈[0,![]() ]时,f(cos2θ-3)+f(4m-2mcosθ)>0对所有的θ均成立,求实数m的取值范围.
]时,f(cos2θ-3)+f(4m-2mcosθ)>0对所有的θ均成立,求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com