以直角坐标系的原点O为极点，x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线I的参数方程为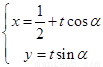（t为参数,O < a <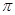),曲线C的极坐标方程为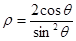

(I)求曲线C的直角坐标方程；

(II)设直线l与曲线C相交于A ,B两点,当a变化时,求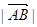的最小值.

如图，直线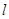与抛物线交于两点，与轴相交于点，且.

（1）求证：点的坐标为；

（2）求证：；

（3）求的面积的最小值.

【解析】设出点M的坐标，并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论，可以设其方程为,然后与抛物线方程联立消x，根据,即可建立关于的方程.求出的值.

（2）在第（1）问的基础上，证明：即可.

（3）先建立面积S关于m的函数关系式，根据建立即可，然后再考虑利用函数求最值的方法求最值.

如图，设抛物线方程为，M为直线上任意一点，过M引抛物

线的切线，切点分别为A，B

（I）求证A，M，B三点的横坐标成等差数列；

（Ⅱ）已知当M点的坐标为（2，一2p）时，．求此时抛物线的方程

（Ⅲ）是否存在点M．使得点C关于直线AB的对称点D在抛物线上，其中，点C满足（O为坐标原点）若存在。求出所有适合题意的点M的坐标；

若不存在，请说明理由。