某校从参加高三年级第一学期期末考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数，满分为100分），将数学成绩进行分组并根据各组人数制成如下频率分布表：

（Ⅰ）将上面的频率分布表补充完整，并估计本次考试全校85分以上学生的比例；

（Ⅱ）为了帮助成绩差的同学提高数学成绩，学校决定成立“二帮一”小组，即从成绩为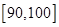中任选出两位同学，共同帮助成绩在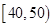中的某一个同学，试列出所有基本事件；若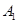同学成绩为43分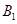，同学成绩为95分，求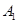、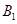两同学恰好被安排在“二帮一”中同一小组的概率．

分 组	频 数	频 率[来源:学_科_网]
[40, 50 ）	2	0.04
[ 50, 60 ）	3	0.06
[ 60, 70 ）	14	0.28
[ 70, 80 ）	15	0.30
[ 80, 90 ）
[ 90, 100 ]	4	0.08
合 计

 

 

 

 

 

 

 

 

 

 

【解析】第一问利用表格可知第五行以此填入  12   0.24

第七行以此填入  50   1   估计本次全校85分以上学生比例为32％

第二问中，设数学成绩在[90，100]间的四个同学分别用字母B1，B2，B3，B4表示；被帮助的两个同学为A₁，A₂出现的“二帮一”小组有A₁B₁B₂；A₁B₁B₃；A₁B₁B₄；A₁B₂B₃；A₁B₂B₄；A₁B₃B₄

A₂B₁B₂；A₂B₁B₃；A₂B₁B₄；A₂B₂B₃；A₂B₂B₄；A₂B₃B₄

A₁、B₁两同学恰好被安排在“二帮一”中同一小组的有   A₁B₁B₂；A₁B₁B₃；A₁B₁B₄

l利用古典概型概率得到。

（Ⅰ）第五行以此填入  12   0.24                ……………2分

第七行以此填入  50   1                  ……………4分

估计本次全校85分以上学生比例为32％                ……………6分

（Ⅱ）设数学成绩在[90，100]间的四个同学分别用字母B₁，B₂，B₃，B₄表示；被帮助的两个同学为A₁，A₂出现的“二帮一”小组有A₁B₁B₂；A₁B₁B₃；A₁B₁B₄；A₁B₂B₃；A₁B₂B₄；A₁B₃B₄

A₂B₁B₂；A₂B₁B₃；A₂B₁B₄；A₂B₂B₃；A₂B₂B₄；A₂B₃B₄

A₁、B₁两同学恰好被安排在“二帮一”中同一小组的有   A₁B₁B₂；A₁B₁B₃；A₁B₁B₄     

所以  A₁、B₁两同学恰好被安排在“二帮一”中同一小组的概率为 3 /12 =1 /4

 

判断下列概率模型是古典概型还是几何概型？

(1)如图3-3-4,转盘上有8个面积相等的扇形,转动转盘,求转盘停止转动时指针落在阴影部分的概率.

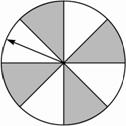
        图3-3-4

(2)在500 mL的水中有一个草履虫,现从中随机取出2 mL水样放到显微镜下观察,求发现草履虫的概率.

下列概率模型中，古典概型的个数为(　　)

(1)从区间[1,10]内任取一个数，求取到1的概率；

(2)从1,2，…，9,10中任取一个整数，求取到1的概率；

(3)向一个正方形ABCD内任意投一点P，求点P刚好与点A重合的概率；

(4)向上抛掷一枚质地不均匀的硬币，求出现反面朝上的概率．

A．1　　　　　　　　　　　      B．2

C．3                            D．4