
题目列表(包括答案和解析)
给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件
②“当x为某一实数时可使 ”是不可能事件
”是不可能事件
③“明天顺德要下雨”是必然事件
④“从100个灯泡中取出5个,5个都是次品”是随机事件.
其中正确命题的个数是 ( )
A.0 B.1 C.2 D.3
给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件
②“当x为某一实数时可使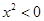 ”是不可能事件
”是不可能事件
③“明天福州要下雨”是必然事件
④李娜在2012年奥运会上,力挫群雄,荣获女子网球单打冠军是随机事件.
其中正确命题的个数是
A. 0 B. 1 C. 2 D. 3
给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件
②“当x为某一实数时可使![]() ”是不可能事件
”是不可能事件
③“明天福州要下雨”是必然事件
④李娜在2012年奥运会上,力挫群雄,荣获女子网球单打冠军是随机事件.
其中正确命题的个数是
A. 0 B. 1 C. 2 D. 3
①至少有一个白球;都是白球 ②至少有一个白球;至少有一个红球 ③恰有一个白球;恰有两个白球 ④至少有一个白球;都是红球
A.0 B.1 C.2 D.3
A.① B.②④ C.③ D.①③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com