练习册

  • 练习册
  • 试题
    一次函数f(x)是R上的增函数且.二次函数g(x)满足.且g(x)的最小值为． 的解析式, (2)当满足时.求函数的值域． 【查看更多】

     

    题目列表(包括答案和解析)

    已知函数f(x)是一次函数且在R上为增函数，若f[f(x)]＝4x＋3．

    (Ⅰ)求f(x)的解析式；

    (Ⅱ)试比较[f(x)]2与f[f(x)]的大小．

    查看答案和解析>>

    已知关于x的函数y=f(x)=a
    x
    3
     
    +b
    x
    2
     
    +cx+d    ，x∈R（a，b，c，d为常数且a≠0），f'（x）=0是关于x的一元二次方程，根的判别式为△，给出下列四个结论：
    ①△＜0是y=f（x）在（-∞，+∞）为单调函数的充要条件；
    ②若x1、x2分别为y=f（x）的极小值点和极大值点，则x2＞x1；
    ③当a＞0，△=0时，f（x）在（-∞，+∞）上单调递增；
    ④当c=3，b=0，a∈（0，1）时，y=f（x）在[-1，1]上单调递减．
    其中正确结论的序号是
     
    ．（填写你认为正确的所有结论序号）

    查看答案和解析>>

     （2010届枣庄市第一次调研）

    已知函数f（x）对任意的实数x、y都有f（x+y） =f（x）+f（y）-1,且当x>0 时,f（x）＞1．

       （1）求证：函数f（x）在R上是增函数；

       （2）若关于x的不等式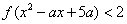的解集为{x|-3＜x＜2＝，求f（2009）的值；

       （3）在（2）的条件下，设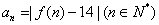,若数列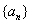从第k项开始的连续20项 之和等于102，求k的值．

     

     

     

     

     

     

     

     

    查看答案和解析>>

    已知以下四个命题：
    ①如果x1，x2是一元二次方程ax2+bx+c=0的两个实根，且x1＜x2，那么不等式ax2+bx+c＜0的解集为{x|x1＜x＜x2}．②若，则（x-1）（x-2）≤0．③“若M={-1，0，1}，则x2-2x+m＞0的解集是实数集R”的逆否命题．④若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
    其中为真命题的是    （填上你认为正确的序号）．

    查看答案和解析>>

    已知以下四个命题：
    ①如果x1，x2是一元二次方程ax2+bx+c=0的两个实根，且x1＜x2，那么不等式ax2+bx+c＜0的解集为{x|x1＜x＜x2}．②若数学公式，则（x-1）（x-2）≤0．③“若M={-1，0，1}，则x2-2x+m＞0的解集是实数集R”的逆否命题．④若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
    其中为真命题的是________（填上你认为正确的序号）．

    查看答案和解析>>


    同步练习册答案