
题目列表(包括答案和解析)
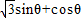 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.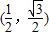 ,求f(θ)的值;
,求f(θ)的值;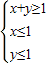 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.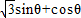 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.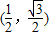 ,求f(θ)的值;
,求f(θ)的值;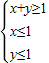 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.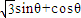 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.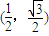 ,求f(θ)的值;
,求f(θ)的值;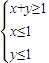 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.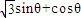 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.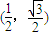 ,求f(θ)的值;
,求f(θ)的值;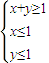 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.一、选择题:(本大题10个小题,每小题5分,共50分)
1--5 BDDCA 6--10 ACBCB
二.填空题:(本大题共6小题,每小题4分,共24分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image295.gif) ;
12.
;
12./file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image297.gif) ; 13.
; 13. /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image299.gif) ; 14.
; 14. /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image301.gif) ;
;
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image303.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image305.gif) ;
;
三、解答题:(本大题共6小题,共76分).
17.(13分)
解:(I)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image307.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image309.gif) ………………………(6分)
………………………(6分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image311.gif) 函数
函数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image076.gif) 的单调减区间为
的单调减区间为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image313.gif) ……………………(7分)
……………………(7分)
(II)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image315.gif) 则
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image076.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image317.gif) ……………(11分)
……………(11分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image311.gif) 函数
函数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image076.gif) 的最大值为
的最大值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image319.gif) ,最小值为
,最小值为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image321.gif) .…………………………(13分)
.…………………………(13分)
18.(13分)
解:(I)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image323.gif) ①
①
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image311.gif) 当
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image325.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image327.gif) ②
②
将①-②得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image329.gif) …………………(4分)
…………………(4分)
在①中,令/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image331.gif) 得
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image333.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image335.gif) ………………………………………………(6分)
………………………………………………(6分)
(II)由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image337.gif) 得
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image339.gif) 则当
则当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image341.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image343.gif) ………(8分)
………(8分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image311.gif) 当
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image325.gif) 时,
时, /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image345.gif) ……………………(9分)
……………………(9分)
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image347.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image349.gif) ……………(12分)
……………(12分)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image343.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image351.gif) …………………………………………(13分)
…………………………………………(13分)
19.(13分)
解:(I)由题意有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image353.gif) ,得
,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image355.gif) ,故
,故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image357.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image359.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image361.gif)
(II)由(I)知:
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image363.gif) ……(11分)
……(11分)
当且仅当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image365.gif) 即
即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image367.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image236.gif) 有最大值.
有最大值.
答: 2009年的年促销费用投入2.5万元时,该厂家利润最大. …………(13分)
20.(13分)
解:(I)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image242.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image244.gif) ,即
,即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image371.gif) (※)
(※)
(1)当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image373.gif) 时,由(※)
时,由(※)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image375.gif)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image373.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image377.gif) ………………………………………………(2分)
………………………………………………(2分)
(2)当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image379.gif) 时,由(※)
时,由(※)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image381.gif)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image379.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image383.gif) ………………………………………(4分)
………………………………………(4分)
(3)当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image385.gif) 时,由(※)
时,由(※)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image387.gif)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image385.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image389.gif) ………………………………………………(6分)
………………………………………………(6分)
综上:由(1)、(2)、(3)知原不等式的解集为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image391.gif) ……………(7分)
……………(7分)
(II)当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image246.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image248.gif) ,即
,即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image393.gif) 恒成立,
恒成立,
也即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image395.gif) 在
在/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image246.gif) 上恒成立。…………………(10分)
上恒成立。…………………(10分)
而/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image397.gif) 在
在/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image399.gif) 上为增函数,故
上为增函数,故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image401.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image403.gif) 当且仅当
当且仅当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image405.gif) 即
即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image407.gif) 时,等号成立.
时,等号成立.
故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image409.gif) …………………………………………………
(13分)
…………………………………………………
(13分)
21.(12分)
解:(I)在/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image411.gif) 中,由余弦定理得
中,由余弦定理得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image413.gif) (1分)
(1分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image415.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image417.gif) ………(4分)
………(4分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image419.gif) ,即动点
,即动点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image256.gif) 的轨迹为以A、B为两焦点的椭圆.
的轨迹为以A、B为两焦点的椭圆.
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image311.gif) 动点
动点/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image256.gif) 的轨迹
的轨迹/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image263.gif) 的方程为:
的方程为:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image422.gif) .………………………… (6分)
.………………………… (6分)
(II)由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image424.gif) 得
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image426.gif) .(※)… (7分)
.(※)… (7分)
设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image428.gif) 、
、/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image430.gif) ,易知
,易知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image432.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image434.gif) ①
①
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image436.gif) ②…………………………………………………(8分)
②…………………………………………………(8分)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image274.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image438.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image440.gif) ③…………………………………………… (10分)
③…………………………………………… (10分)
将③代入①、②得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image442.gif) 消去
消去/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image155.gif) 得
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image445.gif) 或
或/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image447.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image449.gif) ,代入(※)方程
,代入(※)方程/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image451.gif) .故
.故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image445.gif) …………… (12分)
…………… (12分)
22.(12分)
解:(I)由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image454.gif) 得
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image456.gif)
故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image458.gif) ………………………………(2分)
………………………………(2分)
(II)由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image460.gif) 得
得
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image462.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image464.gif) …………(4分)
…………(4分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image466.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image468.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image470.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image472.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image474.gif)
从而/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image476.gif) 即
即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image478.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image480.gif) …………………………………………………(6分)
…………………………………………………(6分)
(III )由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image482.gif) 得
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image484.gif)
设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image486.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image488.gif) 且
且/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image490.gif)
于是/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image492.gif) …………………………………(8分)
…………………………………(8分)
设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image494.gif) 则
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image496.gif) 且
且/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image498.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image500.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr2\6de45fa80c4dddf51d1193e4c60e4a54.zip\65850\重庆市十二校2OO9年高三第一次质量调研抽测试卷(文科综合)\重庆市十二校2OO9年高三第一次质量调研抽测试卷(数学理科).files\image502.gif) ……………(10分)
……………(10分)
从而
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com