
题目列表(包括答案和解析)
已知数列 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列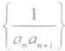 的前100项和为
的前100项和为
(A)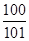 (B)
(B) 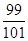 (C)
(C)
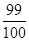 (D)
(D)
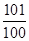
【解析】由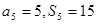 ,得
,得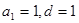 ,所以
,所以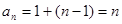 ,所以
,所以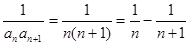 ,又
,又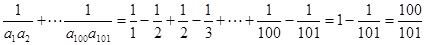 ,选A.
,选A.
数列{an}满足an+1+(-1)n an =2n-1,则{an}的前60项和为
(A)3690 (B)3660 (C)1845 (D)1830
【解析】由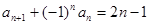 得,
得,
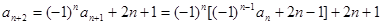
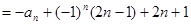 ,
,
即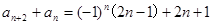 ,也有
,也有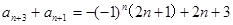 ,两式相加得
,两式相加得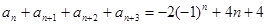 ,设
,设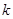 为整数,
为整数,
则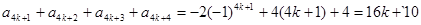 ,
,
于是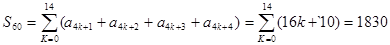
(天津卷理12)一个正方体的各定点均在同一球的球面上,若该球的体积为![]() ,则该正方体的表面积为 .
,则该正方体的表面积为 .
解析:由![]() 得
得![]() ,所以
,所以![]() ,表面积为
,表面积为![]() .
.
(天津卷理12)一个正方体的各定点均在同一球的球面上,若该球的体积为![]() ,则该正方体的表面积为 .
,则该正方体的表面积为 .
解析:由![]() 得
得![]() ,所以
,所以![]() ,表面积为
,表面积为![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com