
题目列表(包括答案和解析)
某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该起市同时一次购进甲、两种商品共80件,恰好用去1600元,求能购进甲乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80元的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案.
青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:

按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一次函数.

(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一次函数.
(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
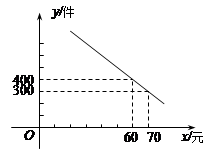
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com